Chapitres
- 01. La première loi de Newton : principe d’inertie ☝?
- 02. La deuxième loi de Newton : la dynamique ✌?
- 03. La troisième loi de Newton : actions réciproques ??
- 04. Principes de la dynamique newtonienne ?
- 05. Les principaux axes pour étudier le mouvement d'un corps ??
- 06. Les énergies mises en jeu lors d'un mouvement ⚡️
Les lois du mouvement de Newton sont un ensemble qui constituent la base de la théorie de Newton sur le mouvement des corps, appelée mécanique newtonienne ou mécanique classique.
- 1️⃣ Première loi de Newton : Tout objet reste au repos ou en mouvement rectiligne uniforme sauf si une force nette agit sur lui.
- 2️⃣ Deuxième loi de Newton : La force appliquée sur un objet est proportionnelle à son accélération, et inversement proportionnelle à sa masse.
- 3️⃣ Troisième loi de Newton : Pour chaque action, il y a une réaction égale et opposée.
Pour en savoir plus sur les trois lois de Newton, on vous propose d'étudier les lois individuellement, les principes de la dynamique newtonienne, ainsi que d'autres principes sur le mouvement et l'énergie des corps.


La première loi de Newton : principe d’inertie ☝?
Tout objet reste au repos ou en mouvement rectiligne uniforme tant qu'aucune force nette n'agit sur lui. Cela signifie qu'un objet ne changera pas son état de mouvement à moins qu'une force nette ne l'ait affecté.
Définition générique de la première loi de Newton (Loi de l'inertie)
Pour démarrer : différence entre système isolé ou pseudo isolé
Un système est isolé s'il n'est soumis à aucune force.
Un système est pseudo isolé si la Σ des forces appliquée à ce système est nulle : Σ F = 0.
Énoncé de la première loi de Newton
Dans un référentiel galiléen (voir la définition plus bas), si la somme vectorielle des forces extérieures qui s'exercent sur un système est nulle (c'est-à-dire si le système est pseudo isolé) alors le vecteur VG du centre d'inertie du système est constant (et réciproquement).
? L’énoncé originel de la première loi de Newton est le suivant : « Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et le contraigne à changer d’état ».
Dans les études de dynamique newtonienne, le référentiel sera dit galiléen (« inertial frame of reference » en anglais) si le principe d’inertie y est vérifié.
On différencie 3 référentiels galiléens en particulier :
Le référentiel de Copernic (ou référentiel héliocentrique) ☀️
Le référentiel terrestre ?
Le référentiel géocentrique ?️
- 1️⃣ Le référentiel de Copernic (dit référentiel héliocentrique) : son origine est au niveau du centre de masse du système solaire (correspondant au centre du Soleil), avec des axes pointant sur 3 étoiles fixes. Il permet l’étude des mouvements des planètes dans le système solaire.
- 2️⃣ Le référentiel terrestre : son origine est au centre de la Terre, avec des axes en rotation
- 3️⃣ Le référentiel géocentrique : son origine est également au centre de la Terre, mais ses axes sont parallèles aux axes du référentiel de Copernic. Il permet l’étude du mouvement des satellites terrestres.
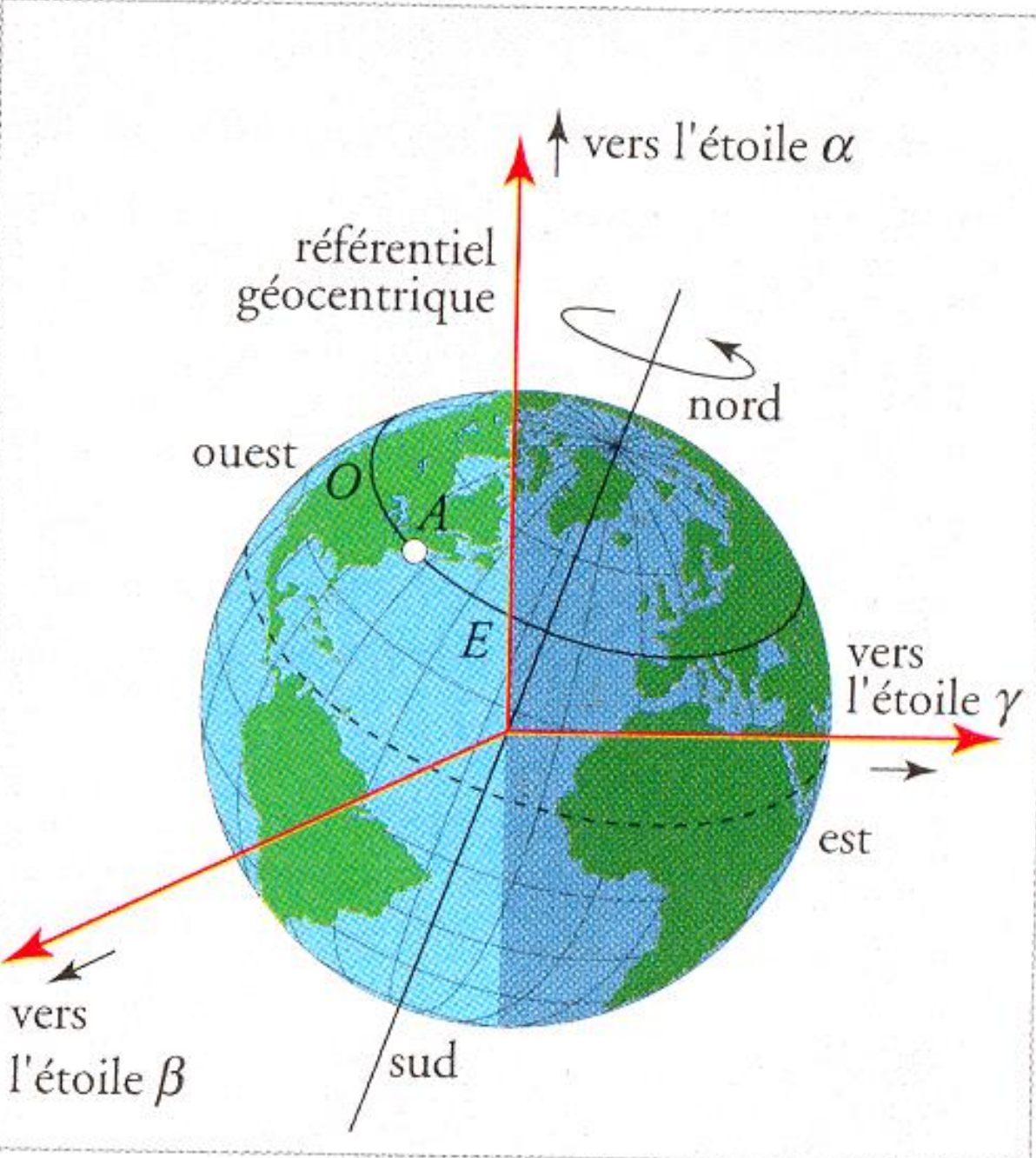
Un énoncé plus moderne du principe d’inertie serait donc : « Dans un référentiel galiléen, si la somme des forces extérieures appliquées à un système mécanique est nulle, alors son centre d’inertie G est au repos ou possède un mouvement rectiligne uniforme. »
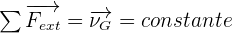
Utilisation de la première loi de Newton
La réciproque de la loi énoncée étant vraie, deux utilisations sont possibles.
Première possibilité
Si les forces qui s'exercent sur un système sont connues, alors la première loi peut être utilisée pour montrer qu'il est en équilibre (immobile) ou qu'il possède un mouvement rectiligne uniforme. Il faut alors montrer que le système n'est soumis à aucune force (il est isolé) ou que les forces auxquelles il est soumis se compensent (il est pseudo isolé) ce qui, dans ce dernier cas, nécessite de faire un bilan des forces.
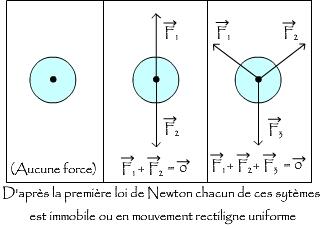
Il est cependant pratiquement impossible pour un objet sur Terre d'être totalement isolé : on le considérera donc pseudo-isolé. C'est le cas d'un objet posé sur une table par exemple : la force de gravité exercée par la Terre sur l'objet est compensée par la force du support.
✅ Exemple pratique
- ⚽️ Imaginez qu'un ballon de football soit posé sur le sol. Il est immobile et reste à sa place, car aucune force ne s'applique dessus. Mais si quelqu'un venait à donner un coup de pied dans le ballon, il va bouger en suivant la direction et la vitesse du coup de pied.
- Maintenant, si le ballon roule sur un terrain plat, il va continuer à rouler jusqu'à ce qu'une force s'applique sur lui, comme par exemple un joueur qui le stoppe avec son pied ou qu'il rencontre un obstacle sur son chemin.
- Dans ces deux exemples, le ballon reste immobile ou en mouvement uniforme tant qu'aucune force nette n'agit sur lui. Cela illustre la première loi de Newton, qui nous dit que tout objet reste au repos ou en mouvement rectiligne uniforme tant qu'aucune force nette n'agit sur lui.
Deuxième possibilité
Si l'on sait qu'un solide est immobile ou en mouvement rectiligne uniforme, alors la première loi de Newton peut être utilisée pour montrer qu'un système est isolé ou pseudo-isolé. Dans ce dernier cas, la somme vectorielle des forces est nulle et il est alors possible de déterminer les caractéristiques d'une des forces appliquées au système si les autres sont connues.
Par exemple, si un système immobile est soumis à 3 forces F1, F2 et F3, d’après la réciproque de la première loi de Newton :
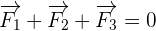
La deuxième loi de Newton : la dynamique ✌?
La force appliquée sur un objet est proportionnelle à la masse de l’objet et à l’accélération qu’il subit. Cela signifie que plus la force appliquée est grande, plus l'objet accélère ; et pour une même force, plus l’objet est lourd, moins il accélère rapidement.
Définition générique de la deuxième loi de Newton (Loi fondamentale de la dynamique)
Dans un référentiel galiléen, si la somme vectorielle des forces appliquées à un système est non nulle, alors le vecteur vitesse du centre d'inertie du système varie. Le vecteur variation de vitesse du centre d'inertie et la somme vectorielle des forces extérieures appliqués au système ont même direction et même sens.
? L’énoncé original de la deuxième loi de Newton est le suivant : « Les changements qui arrivent dans le mouvement sont proportionnels à la force motrice ; et se font dans la ligne droite dans laquelle cette force a été imprimée »
Le mouvement des corps est provoqué par l’application d’une force extérieure sur l’objet, qui correspond à une grandeur vectorielle Fext ayant une direction, un sens et une intensité traduite par une norme. Cette force, dont l’intensité est exprimée en newton (N), traduit les « efforts » mis en œuvre pour mettre en mouvement l’objet : lorsqu’une action extérieure est exercée sur un corps, le mouvement de ce corps (et donc sa vitesse) est modifiée. Une accélération non nulle apparaît alors sous l’effet de la force.
? On peut donc comprendre l’énoncé de la manière suivante : « Dans un référentiel galiléen, la somme vectorielle des force extérieures (notée ∑Fext) exercées sur un système ponctuel est égale à la dérivée du vecteur quantité de mouvement de ce système par rapport au temps. »
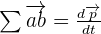
Utilisation de la deuxième loi de Newton
Le plus souvent, cette loi est utilisée pour des "systèmes fermés", c'est à dire des systèmes dont la masse (m) est constante. La masse est ici définie comme la quantité de matière contenue dans un corps. Son unité est le kilogramme (kg).
Dans ce cas, la loi se simplifie :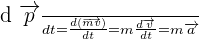
Dans le cas d'un système fermé, la force résultante F exercée sur un point matériel, de masse m donnée, est égale au produit de la masse du point et de son accélération a.
Cette expression permet également d'affirmer que plus la masse d'un objet est élevée, plus son accélération sera faible : la masse est inversement proportionnelle à l'accélération. De même, la masse s'opposant à la variation de vitesse, plus elle sera élevée, plus l'inertie sera importante.
Il est important de noter que dans le cas où 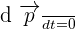
Alors
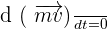
Cela qui signifie que la vitesse est constante. On se retrouve donc dans une situation identique à la première loi de Newton.
Cette expression de la deuxième loi de Newton permet de déterminer la valeur de l'accélération à partir des forces qui s'exercent sur le système. Une fois l'accélération connue, il est possible de déterminer la vitesse, puis les coordonnées du système au cours du temps.
En général, on utilise cette expression en projetant les vecteurs sur les axes d'un repère.
Par exemple dans le cas d'un système soumis à trois forces dans un repère cartésien on obtient les équations suivantes :
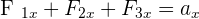

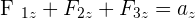
✅ Exemple pratique
- ? Si vous poussez un chariot de supermarché vide et un chariot de supermarché rempli de produits, vous remarquerez que le chariot rempli de produits est plus difficile à pousser que le chariot vide.
- Cela est dû à la deuxième loi de Newton, qui indique que la force nécessaire pour accélérer un objet dépend de sa masse. Le chariot rempli de produits a une masse plus grande que le chariot vide, donc il nécessite plus de force pour être déplacé. C'est pourquoi il est plus difficile à pousser.
La troisième loi de Newton : actions réciproques ??
Pour chaque action, il y a une réaction égale et opposée. Cela signifie que chaque fois qu'une force est appliquée sur un objet, cet objet applique une force de même magnitude mais en direction opposée sur l'objet exerçant la force.
Définition générique de la Troisième loi de Newton (Loi de l'action et de la réaction)

Cette loi aussi appelée « principe des actions réciproques » ou « loi de l'action et de la réaction ».
Si un système A exerce une action mécanique sur un système B, modélisée par la force FA/B, alors le système B exercent une action mécanique sur, modélisée par la force FA/B telle que FA/B = - FA/B
? L’énoncé original de la troisième loi de Newton est le suivant : « L’action est toujours égale à la réaction, c’est-à-dire que les actions de deux corps l’un sur l’autre sont toujours égales et de sens contraires »
Cet énoncé se traduit de la façon suivante : Soit A et B deux corps en interaction. Si un système A exerce une force FA/B sur un système B, alors le système B exerce aussi sur le système A une force FB/A ayant même droite de direction mais un sens opposé.
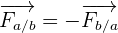
Cette loi est valable pour toutes les forces, qu’elles s’exercent à distance ou par contact.

C'est cette loi qui s'observe lorsque qu'un aimant et un morceau de fer de même masse se font face. L'aimant et le morceau de fer seront "attirés" l'un vers l'autre avec la même vitesse, ce qui montre qu'ils sont soumis à des forces égales et opposées. Ces deux éléments vont donc entrer en collision, puis s'immobiliser.
Il est cependant important de ne pas oublier que les deux forces évoquées ne s'annulent pas entre elles.
✅ Exemple pratique
- ?? Si vous appuyez sur un mur, le mur pousse également contre vous avec une force égale et opposée. Cette force est appelée force de réaction. Cela signifie que chaque action a une réaction égale et opposée. Cela peut sembler contre-intuitif, car on pourrait penser que le mur ne bouge pas.
- Mais, en réalité, le mur exerce une force sur vous, qui est égale et opposée à la force que vous exercez sur le mur. C'est un exemple de la troisième loi de Newton, qui décrit les actions réciproques entre deux objets en interaction.
Principes de la dynamique newtonienne ?
La dynamique newtonienne (ou dynamique du point matériel) est une partie indispensable de la mécanique, et donc de l’étude du mouvement dans un référentiel galiléen. Ne pas confondre :
✅ Mécanique newtonienne
Elle permet d’étudier les mouvements d’objets macroscopiques se déplaçant à des vitesses inférieures à celle de la lumière
❌ Mécanique quantique
Elle étudie les mouvements des particules et objets à très grande vitesse.
? Tous ces principes ont été regroupés dans l’ouvrage Principes mathématiques de la philosophie naturelle, écrit par Isaac Newton en 1686.
Il est important de noter que ces principes, de par leur nature, ne se démontrent pas.
L'inertie d'un corps

En physique, on appelle inertie d'un corps, dans un référentiel galiléen, une tendance de ce corps à conserver sa vitesse. En effet, lorsqu'il y a absence d'influences extérieures, on parle aussi de forces extérieures, alors tout corps que l'on considère comme ponctuel va perdurer dans un mouvement rectiligne uniforme.
? Notons que l'on appelle aussi l'inertie, principe d'inertie ou encore loi d'inertie.
Puis, lorsque Newton est arrivé, on l'appelle également première loi de Newton.
Notion de référentiel
Un référentiel d’étude est le solide par rapport auquel le mouvement d’un corps sera décrit. C’est dans ce référentiel que sera définit le repère d’espace qui sera utilisé pour suivre le mouvement, parmi l’infinité de repères existants.
Le plus souvent, ce repère sera cartésien et orthonormé. Un point M y sera repéré par 3 coordonnées (x, y, z). Ces 3 coordonnées sont fonction du temps : c’est le vecteur position OM, dont l’unité est le mètre.
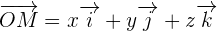
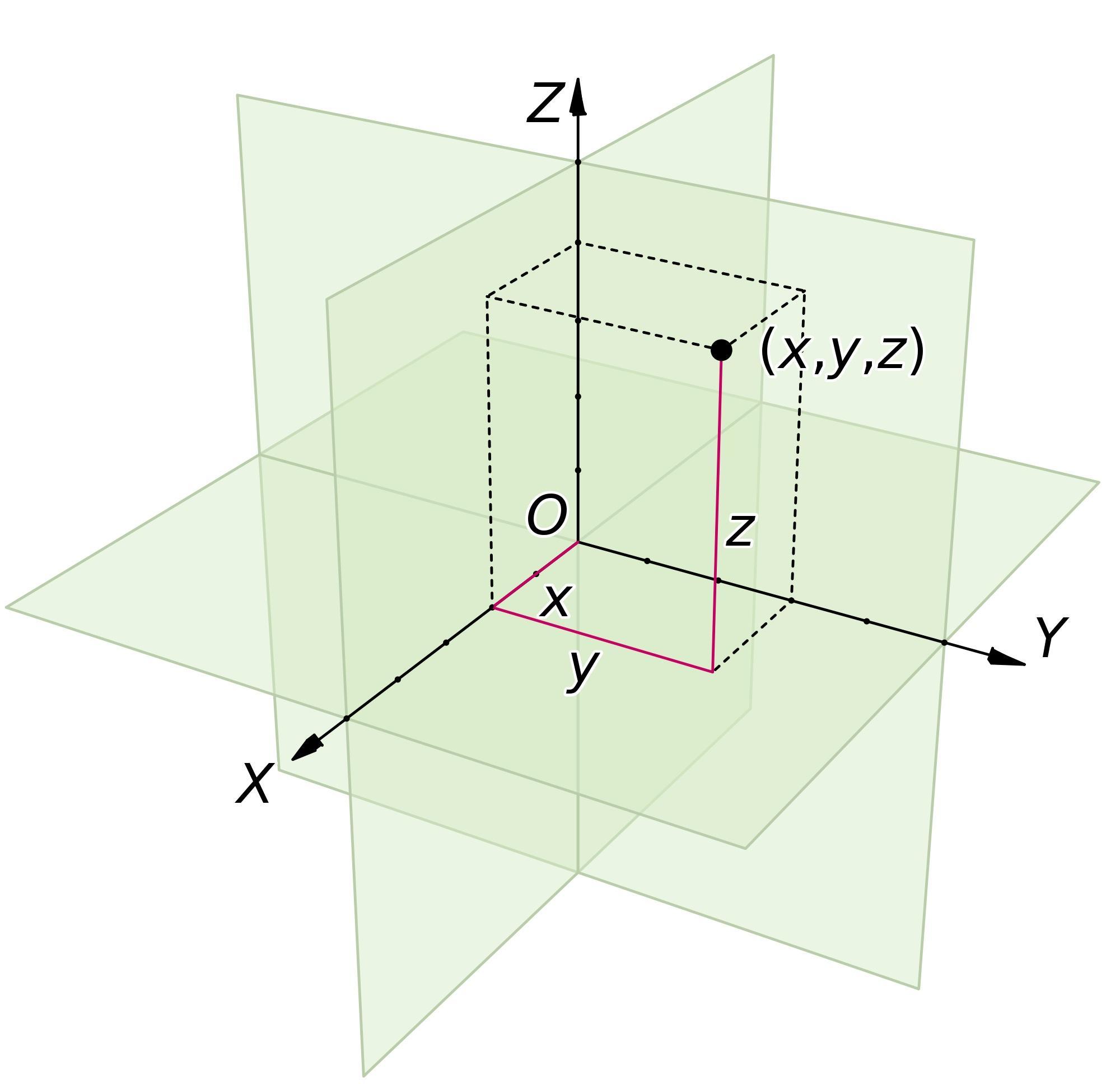
Le référentiel galiléen
Un référentiel est un solide par rapport auquel on étudie un mouvement On prend souvent comme référentiel le solide Terre (galiléen), mais parfois le soleil (héliocentrique) ou spatial.
Un repère d'espace orthonormé, lié à un référentiel, est un système d'axes orthogonaux et normés, muni d'une origine O. Dans ce repère, on peut exprimer les coordonnées du mobile ponctuel étudié. La trajectoire d'un mobile ponctuel est constituée par l'ensemble des positions successives occupées par le mobile au cours du temps.
Pour calculer la vitesse v moyenne entre deux instants d'un solide, on utilise la formule suivante :
- ?️ Vitesse moyenne (m/s) = distance parcourue (m) / durée du parcours (s)
- ?️ Vecteur vitesse instantanée = dérivée du vecteur position par rapport au temps
Ce vecteur est porté par la tangente à la trajectoire à la date considérée et a toujours le sens du mouvement.
Dans un référentiel galiléen, si la somme vectorielle des forces extérieures appliquées à un solide est nulle (solide pseudo-isolé) alors le centre d'inertie G de ce solide est soit au repos, soit animé d'un mouvement rectiligne uniforme et réciproquement. Un solide peut donc se déplacer même si la somme des forces appliquées à ce solide soit nulle. Dans un référentiel galiléen, si le vecteur vitesse du centre d'inertie d'un solide varie, alors la somme vectorielle des forces extérieures appliquées à ce solide n'est pas nulle et réciproquement.
La direction et le sens de cette somme sont ceux de la variation du vecteur vitesse entre deux instants proches. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie.
Vecteur quantité de mouvement
Le vecteur quantité de mouvement p (kg.m.s-1) d’un point matériel M de masse m se déplaçant à la vitesse VM/R0 par rapport à un espace de référence R0 est :
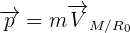
C’est un vecteur dépendant du référentiel d’étude, colinéaire au vecteur vitesse VM/R0, et donc tangent à la trajectoire du point M.
Dans un référentiel galiléen, le vecteur quantité de mouvement d’un système isolé est constant, ce qui explique les phénomènes de propulsions par réaction.
Vecteur de vitesse

Le vecteur vitesse, utilisé dans la définition du vecteur p est la dérivée du vecteur position OM par rapport au temps :
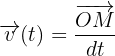
C’est un vecteur dont la direction est une droite tangente à la trajectoire au point M. Son sens est celui du mouvement, et il s’applique au point M. Sa norme, exprimée en m.s-1, est égale à :
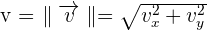
Enfin, le vecteur vitesse moyenne est égal à :
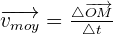
Vecteur accélération
Le vecteur accélération au point M, noté a, caractérise la variation du vecteur vitesse par rapport au temps.
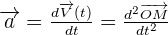
Il est de même direction et même sens que le vecteur vitesse, s’applique au point M et possède une norme exprimée en m.s-2 égale à :

Les principaux axes pour étudier le mouvement d'un corps ??

? Lorsqu’un solide est soumis à des actions extérieures qui se compensent on dit qu’il est pseudo-isolé. Un solide qui ne subirait aucune action extérieure serait dit isolé, ce serait approximativement le cas d’un solide perdu, très très loin de toute étoile ou planète, dans l’espace interstellaire.
? Le centre d’inertie d'un objet, et ce quelle que soit l’histoire antérieure du système, s’il est pseudo isolé, correspond à un et un seul des points de sa trajectoire qui est toujours en mouvement rectiligne et uniforme. C’est par exemple au centre d’inertie d’un solide que s’exerce le poids du système.
↔️ On dit que deux objets A et B sont en interaction, si l'objet A exerce une action qui se manifeste par ses effets sur l'objet B, et si réciproquement, l'objet B agit sur l'objet A.
On considère qu'une force correspond à l’action exercée par chacun des corps sur l’autre.
?? Puisque toute interaction est réciproque, on choisit d’étudier un participant, le système, et les forces qui s’exercent sur lui. Un système correspond à l’ensembles des objets dont on étudie le mouvement. Ainsi on sépare l’Univers en deux : le système et l’extérieur.
Pour résumer, tout ce qui n’est pas le système est appelé extérieur et le système subit des forces exercées par ce qui est intérieur au système, appelées forces extérieures.

- Qu’est-ce qu’un système déformable ?
- Un système déformable correspond système dont la distance entre deux de ces points quelconques peur varier.
- Qu’est-ce qu’un système indéformable ?
- Un système indéformable correspond à un système dont la distance entre deux de ce point quelconque est toujours constante. Un tel système est alors appelé un solide.
On considère qu'une force localisée correspond à une force qui ne s’applique qu'en un point d’un objet ou sur un objet ponctuel. Par exemple un fil tire un objet avec une force T localisée au point d’accrochage
On considère qu'une force répartie correspond à une force qui s’applique sur un ensemble de points répartis sur une surface ou dans un volume de l’objet. Par exemple le poids P est réparti dans tout le volume d’un objet.
On considère qu'une force à distance correspond à une force qui s’exerce entre 2 objets pouvant être séparés par de l’air, de l’eau, du vide… Il y a 3 sortes de forces à distance :
- Pour considérer une force comme étant une force de contact, il faut obligatoirement qu’il y ait contact entre les deux objets pour que naisse cette fameuse force de contact. Par exemple la force de traction d’un fil, mesurée par la tension du fil, s’applique au point de contact objet-fil.
- Un effet dynamique correspond à une force qui peut modifier le mouvement d’un système, c’est à dire modifier son vecteur vitesse.
- Les effets statiques existant sont :
- L'équilibre : on considère qu'un système est en équilibre si tous ses points sont au repos dans le référentiel d’étude.
- Les effets d’une force : on considère qu’une force peut contribuer à l’équilibre d’un système et déformer un système en équilibre ou non.
- Qu’est-ce qu’un solide ponctuel ?
- Un solide ponctuel correspond à un solide dont les dimensions sont très inférieures aux autres dimensions du problème et qui peut donc être considéré comme un point.
Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par rapport auquel on étudiera le mouvement de notre système.
? Définition : La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
En simplifiant, on peut définir le référentiel comme quelque chose correspondant au milieu au sein duquel on étudie le mouvement. En effet, si nous choisissons de prendre l'exemple du voyageur assit dans un train en marche alors le référentiel vas changer selon l'observateur :
- Par rapport à un observateur sur le quai, le voyageur est en mouvement
- Par rapport à un observateur dans le train, le voyageur est immobile.
Ainsi, il est possible de conclure que, pour décrire le mouvement d’un mobile, il faut choisir un repère d’espace ou référentiel. La trajectoire correspond à l’ensemble de toutes les positions successives qu’occupe un point du mobile au cours du temps. La trajectoire peut être curviligne, c'est à dire en vague, circulaire, donc en forme de rond, ou rectiligne.
- Mouvement rectiligne : la trajectoire est une droite
- Mouvement circulaire : la trajectoire est un arc de cercle
- Mouvement curviligne : la trajectoire est une courbe quelconque, plane ou non.
Deux types de mouvements sont très importants dans l’étude des systèmes :
- La translation : Dans un mouvement de translation, chaque segment de droite, appartenant au mobile, reste parallèle à lui-même, au cours du déplacement et tous les points du mobile ont des trajectoires identiques de même longueur.
- La rotation : Dans un mouvement de rotation, tous les points du mobile décrivent des cercles ou des arcs de cercles centrés sur une droite fixe que l'on appelle axe de rotation. On peut notamment illustrer ce mouvement avec l'exemple des aiguilles d’une horloge.
- Si la trajectoire est une droite, la translation est rectiligne, comme dans le cas d'un ascenseur.
- Si la trajectoire est une courbe, la translation est curviligne, comme dans le cas d'un téléphérique.
- Si la trajectoire est un cercle ou un arc de cercle, la translation est circulaire, comme dans le cas d'une grande roue.
? Définition : Une translation correspond à une droite passant par 2 points quelconques du solide qui reste parallèle au cours du mouvement
? Définition : Une rotation correspond à un mouvement où tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
Les énergies mises en jeu lors d'un mouvement ⚡️
L'énergie cinétique
Tout corps en mouvement en possède une. Elle peut être macroscopique : elle dépend alors de la vitesse du corps en mouvement, et donc du référentiel d'étude microscopique : elle est liée à l'agitation moléculaire. Une augmentation de l'énergie cinétique microscopique se traduit par une augmentation de la température. En résumé, l'énergie cinétique correspond à l'énergie d'un objet en mouvement.
La formule est :
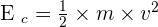
Avec :
- Ec correspondant à l'énergie cinétique de l'objet étudié avec pour unité le Joule noté J ;
- m correspondant à la masse de l'objet étudié avec pour unité le kilogramme noté kg ;
- Et v correspondant à la vitesse de l'objet étudié avec pour unité la mètre par seconde noté m.s-1.
✅ Exemple
Prenons le cas d'un système en translation. Il est important de savoir que la relation définissant l'énergie cinétique ne s'applique pas pour les solides en rotation. L'énergie cinétique d'une voiture qui pèse 1 tonne et qui roule à 130 Km/h est de  .
.
Énergie cinétique : la vitesse

La vitesse est une grandeur physique qui est définie par une évolution face au temps. La vitesse ne définit pas qu’uniquement la vitesse de déplacement mais peut aussi correspondre à la vitesse de réaction chimique ou encore une vitesse de séchage par exemple.
En règle générale, une vitesse est égale à la division de la mesure d’une variation telle qu’une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation. L’exemple le plus simple est celui de la vitesse de déplacement. Il s’agit d’une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.
Énergie cinétique : la masse
En physique, la masse correspond à une grandeur physique positive et intrinsèque d'un corps. De façon plus précise, en physique newtonienne, la masse correspond à une grandeur extensive. Cela signifie alors que la masse d'un corps formé de parties correspond à la somme des masses de ces différentes parties qui le compose.
De plus, il est essentiel de noter que la masse est une grandeur conservative. De ce fait, elle reste constante dans le cas d'un système isolé qui n'échange donc pas de matière avec son environnement.
L'énergie potentielle (ou de position)
Elle dépend de la position relative des différentes parties du système : seul un système déformable pourra posséder, à l'échelle macroscopique, de l'énergie potentielle. En résumé, l'énergie potentielle correspond à l'énergie contenue dans un objet au-dessus du sol. La formule est : \[ E _ { p } = m \times g \times h \]
- Ep correspondant à l'énergie potentielle de l'objet étudié avec pour unité le Joule noté J ;
- m correspondant à la masse de l'objet étudié avec pour unité le kilogramme noté kg ;
- g correspondant à l'intensité de pesanteur avec pour unité le Newton par kilogramme noté N.kg-1. A noter que la valeur approximative de g est de 9,81 N.kg-1.
- Et v correspondant à la vitesse de l'objet étudié avec pour unité la mètre par seconde noté m.s-1.
L'énergie mécanique
L'énergie mécanique Em d'un système est une grandeur macroscopique, somme de son énergie cinétique Ec et de son énergie potentielle Ep. 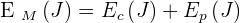 L'énergie mécanique dépend alors du référentiel d'étude.
L'énergie mécanique dépend alors du référentiel d'étude.
Vous savez désormais tout sur les trois lois de Newton !
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Il y a une erreur sur la deuxième loi de Newton, la force est directement proportionnelle à la masse et l’accélération, et non inversement prop.
Bonjour, merci pour votre commentaire qui nous a permis de corriger cette erreur. Belle journée à vous :)
Merci, sans doute vous êtes très aidants je été impressionné. C’est plutôt sympa.
Il est indiqué, au tout début dans l’énoncé de la deuxième loi, qu’une force exercée sur un objet est inversement proportionnelle à sa masse. Ce qui est faux : la force est proportionnelle à sa masse tout comme à son accélération :
F=m.a
Dans énergie potentielle ou de position (dans la légende),il s’agit plutôt de h que de v.
mes remerciements pour l’article.
p=m1/2distance
Merci beaucoup pour l’information.sinon j’aimerais savoir la relation entre les trois lois de Newton dans la basse cylindrique, sphérique et cartésien
Bonjour, nous serions ravis de vous aider ! Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique « Découvrir nos Superprofs » en indiquant la physique. Vous trouverez de nombreux professeurs près de chez vous. Bonne journée ! 🙂