Chapitres
Le travail d'une force est une notion importante en physique qui mesure l'effet d'une force sur un objet lorsqu'il se déplace
Pour traduire l'effet d'une force constante sur un système, on définit une nouvelle grandeur qui tient compte des 3 facteurs suivants :
- Intensité de la force ;
- Angle entre la force et la trajectoire (le cosinus) ;
- Déplacement du point d'application de la force.
Imaginez que vous poussez un chariot sur une distance. Si :
➡️ Vous exercez une force dans la direction du déplacement, vous effectuez un travail positif en transférant de l'énergie au chariot
⬅️ Vous tirez le chariot dans la direction opposée, votre travail sera négatif car vous lui enlevez de l'énergie
Le travail est calculé en multipliant la force par la distance parcourue dans la direction de la force.
C'est un concept clé pour comprendre comment les forces interagissent avec les objets et modifient leur énergie

Qu'est-ce le travail d'une force ?

Le travail d'une force traduit les échanges d'énergie qui s'opèrent sur un système en mouvement d'un point A vers un point B
Cette notion a été introduite pour la première fois par Gaspard-Gustave Coriolis (polytechnicien français) au début du XIXe siècle pour affiner la notion de ce qui était alors appelé "puissance mécanique".
Cette appellation mal définie entraînait des approximations lors d'études mécaniques.
Notation et unité

Le travail d'une force qui s'exerce sur un système ne peut s'exprimer que lorsque ce système est en mouvement. Si par exemple le système se déplace d'un point A à un point B, alors le travail se note :
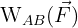
Le travail s'exprime dans la même unité que l'énergie, en général en joules (ce sont également des Newtons par mètre).
Voici quelques exemples de transfert d'énergie nécessaires à une action :
| Action | Energie pour soulever une pomme de 100 g d'1 mètre sur Terre | Energie nécessaire à un enfant de 30 kg pour monter à l'étage (environ 3 m) | Energie nécessaire à un rugbyman de 100 kg pour effectuer un course de 50 m | Energie nécessaire à un cycliste pour effectuer 25 km sur le plat |
|---|---|---|---|---|
| Ordre de grandeur en joule | 1 | 1000 | 5000 | 500 000 |
Les différents types de travail d'une force

Travail d'une force conservative
Par définition, une force est dite conservative si son travail ne dépend pas du chemin suivi par le système en mouvement.
Quel que soit le chemin suivi pour aller d'un point A à un point B, le travail de cette force a toujours pour expression le produit scalaire du vecteur force par le vecteur trajectoire :
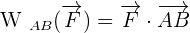
- avec la force F en Newtons
- et le chemin AB en mètres
Les principales forces conservatives sont :
Les forces gravitationnelles (poids)
⚡️ Les forces électrostatiques
Travail d'une force constante lors d'un déplacement rectiligne
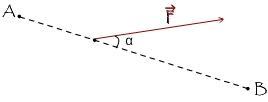
Si un système est soumis à une force constante lors d'un trajet rectiligne d'un point A à un point B, on considère alors la force constante comme conservative, et le travail de cette force correspond à la formule vue plus haut :

Pour quantifier le travail de la force, il faut alors connaître les normes (distances) des vecteurs.
Si l'angle entre les deux vecteurs est noté α, alors l'expression du travail devient :

Cas particuliers de travaux de forces constantes lors d'un déplacement rectiligne
Voici quelques cas particuliers d'angles, très souvent rencontrés :
- Si α = 90° alors cos (90) = 0 donc le travail est nul (Toute force perpendiculaire à la trajectoire a un travail nul car un produit scalaire est nul lorsque deux vecteurs sont à 90°).
- Si α < 90° alors cos (α) > 0 et la valeur du travail est positive : il s'agit d'un travail moteur.
- Si α > 90° alors cos (α) < 0 et la valeur du travail est négative : il s'agit d'un travail résistant.
- Si α = 0 alors cos (0) = 1 et alors WAB = F x AB.
- Si α = 180° alors cos (180) = -1 et alors WAB = - F x AB.
Le travail d'une force non constante
Lorsque le travail d'une force n'est pas constant, cela signifie que l'intensité de cette force varie tout au long du déplacement.
Prenons l'exemple d'un objet que l'on soulève verticalement. Au fur et à mesure que l'objet monte, le travail de la force gravitationnelle augmente car la distance parcourue est plus grande. Si l'objet est soulevé plus rapidement, la force exercée pour le maintenir en mouvement est également plus grande, augmentant le travail total.
✅ Ainsi, le travail d'une force non constante dépend de la variation de l'intensité de la force tout au long du déplacement
Cela peut être illustré par des situations où la force appliquée change en fonction du temps, de la position ou de la vitesse de l'objet.
Travail d'une force lors d'un mouvement circulaire

Si le système étudié est une grande roue tournant sur son axe, la force qui s'exerce sur le point de fixation d'une nacelle, est la force centripète.
Son vecteur force est de même sens et direction que le vecteur accélération (dite accélération centripète). Ce vecteur est selon le diamètre de la grande roue et est dirigé vers le centre. Ceci signifie que le vecteur de la force centripète est perpendiculaire en tout point de la trajectoire.
✅ Le travail de la force est nul car le produit scalaire de deux vecteurs perpendiculaires est toujours nul
Ceci explique que la roue tourne sur elle-même et que le centre de rotation reste immobile.
Dans le cas d'une roue de voiture ou d'une roue de vélo en descente, la force centripète n'est pas la seule à s'exercer sur la roue (force du moteur du véhicule ou poids pour le vélo en descente), ce qui explique le mouvement. La force centripète, à l'origine de la rotation de la roue, aura toujours un travail nul.
Le travail d'une force lors d'un mouvement curviligne
Lors d'un mouvement curviligne, le travail d'une force mesure l'effet de cette force sur un objet qui se déplace le long d'une trajectoire courbe.
Prenons l'exemple d'une balle attachée à une ficelle que l'on fait tourner en cercle. La force exercée par la ficelle vers le centre est appelée force centripète. Bien que la trajectoire soit courbe, le travail de cette force centripète est nul car elle est perpendiculaire au déplacement.
Cependant, si une autre force, comme la gravité, agit dans la direction du déplacement, elle effectuera un travail en transférant de l'énergie à la balle, ce qui affectera sa vitesse ou sa hauteur.
✅ Lors d'un mouvement curviligne, le travail dépend des forces présentes et de leur orientation par rapport à la trajectoire
Cela implique de prendre en compte la composante tangentielle et la composante normale de la force par rapport au déplacement.
Le travail d'une force élastique
Les forces élastiques, telles que celles exercées par les ressorts, peuvent également effectuer du travail.
Il est important de comprendre comment calculer le travail dans ces situations, en utilisant la loi de Hooke et la déformation du ressort.

Le travail d'une force élastique se produit lorsque l'on étire ou compresse un ressort :
- Lorsque l'on déforme un ressort, il exerce une force opposée à la déformation, appelée force élastique
- Si on étire le ressort, la force élastique tire l'objet vers l'arrière, effectuant un travail positif
- Si on compresse le ressort, la force élastique pousse l'objet vers l'avant, effectuant un travail négatif
✅ Le travail total de la force élastique dépend de la déformation du ressort et peut être calculé en multipliant la force élastique par la distance de déformation
Cela peut être illustré par des exemples tels que le lancement d'une catapulte ou le rebondissement d'un trampoline.
Le travail d'une force en pratique : puissance, vitesse, poids
Dans la réalité, il n'est pas rare de constater que plus d'une force s'applique au corps étudié. En effet, un cycliste lancé dans une pente va pouvoir également pédaler. En plus du travail de la force du poids du système cycliste + vélo, s'ajoute la force motrice apportée par le cycliste appuyant sur les pédales.
Si différentes forces sont appliquées à des points effectuant tous le même trajet de A vers B, les travaux des forces s'additionnent :

⚠️ À noter que les travaux de chaque force s'additionnent algébriquement, ce qui signifie que si les forces sont de mêmes intensités mais de sens opposés, alors le travail total est nul.
Le rôle de la puissance
Le travail d’une force correspond au transfert d’énergie nécessaire pour déplacer un objet. Cependant, il ne rend pas compte de l'énergie nécessaire pour effectuer ce déplacement en un temps donné (vitesse).
La puissance d'une force rend compte de la rapidité du transfert d'énergie et donc tient compte du temps nécessaire à la réalisation du déplacement (vitesse).
L'expression de la puissance est la suivante :
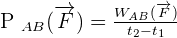
Si les forces s'exercent sur des points effectuant le même trajet de A vers B, alors les travaux s'additionneront et la puissance totale pourra être calculée de la manière suivante :
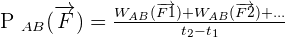
Les unités classiques de mesure de puissance sont des watts (Joules par seconde).
Exemples de puissances lors de mouvement rectiligne uniforme

La puissance, en physique, permet d'indiquer la vitesse à laquelle un travail est fourni
Cela correspond alors à la quantité d'énergie par unité de temps fournie par un système à un autre système. On peut donc conclure que la puissance correspond à une grandeur scalaire et à un débit d'énergie.
Si deux systèmes de puissances différentes fournissent le même travail, et donc la même énergie, ce sera le plus puissant des deux systèmes qui sera donc le plus rapide.
On peut exprimer la capacité d'un système à fournir un travail en un temps donné à l'aide du rapport suivant :

On peut déduire de cette formule, que l'intégrale de la puissance fournie par rapport au temps représente alors le travail fourni par le système. En ce qui concerne la notation et les unités, dans le SIU, le système international d'unité, une puissance s'exprime en watts, en joules par seconde ou encore en kg.m2.s-3. Autrefois, on utilisait encore le cheval-vapeur, cette unité comparait alors la traction d'une machine à vapeur à celle d'un cheval de trait.
La puissance est une grandeur très utilisée pour comparer des véhicules. Si l'unité généralement utilisée est l'unité historique du cheval vapeur, nous exprimerons ici la puissance en watt.
Comparons les puissances au démarrage de deux Formules 1 sur la ligne de départ d'un circuit :
- Le travail du moteur de chacune est de 3,3 MJ
- Cependant les mécaniques de ces deux formules 1 sont différentes.
Ainsi :
- Le démarrage de la première Formule 1 est plus performant et cette voiture parcourt 150 mètres en 5 secondes
- La seconde Formule 1 parcourt 150 mètres en 5,5 secondes
Calculons maintenant les puissances déployées par ces deux véhicules :

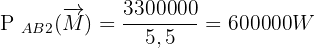
Pour un même travail, la seconde Formule 1 est moins puissante car son transfert d'énergie est plus lent
Le Système International d'Unités
L'ensemble des unités associées aux dimensions fondamentales constitue le Système International d'Unités.
Il s'agit du système MksA (mètre, kilogramme, seconde, Ampère), mais le Kelvin, le mole et le candela font aussi partie de ce système. Ces unités sont appelées unités légales. Elles sont universelles et connues de par le monde entier.
Il est important de savoir que toutes les autres dimensions se déduisent de ces sept dimensions fondamentales par produit ou division de ces dimensions.
Dans certains sujets d'exercices, les grandeurs ne sont pas exprimées dans le système international mais avec des grandeurs usuelles. Il est facile de les comprendre et elles sont parfois utilisées dans la vie de tous les jours, mais il est essentiel de toujours effectuer les calculs avec les grandeurs exprimées dans l'unité internationale pour éviter les erreurs.
Définissons quelques variables associées à la puissance

Vitesse de transformation
Puisque la puissance est une grandeur physique, celle-ci reflète alors la notion de changement matériel dans l'univers mais également le temps nécessaire afin que ce changement s'effectue.
❌ Ainsi, la puissance est différent du travail puisque celui-ci prend uniquement en compte le changement et non pas la durée nécessaire à ce changement
De ce fait, pour un même travail effectué lorsqu'une charge pesante est transportée en haut d'un escalier, la puissance sera différente selon si le porteur de la charge effectue cette tâche en courant ou en marchant.
En effet, dans le cas où le porteur transporte sa charge en courant, la puissance nécessaire à l'exécution de cette action est beaucoup plus grande. Ceci est encore plus vrai lorsque le délai d'accomplissement de ce travail est plus faible.
On peut également illustrer cela en se basant sur l'exemple de la combustion complète d'un kilogramme de charbon. En effet, celle-ci libère plus d'énergie que l'explosion d'un kilogramme de TNT : l'explosion de TNT produit environ 4,7 mégaJoules par kilogramme alors que la combustion du charbon produit entre 15 et 30 mégaJoules par kilogramme.
La principale différence entre ces deux réactions est la différence de puissance : puisque l'explosion est un phénomène beaucoup plus rapide que la combustion, la puissance de la première réaction est beaucoup plus supérieure que celle de la deuxième pour un même poids de réactif même si l'énergie intrinsèque du charbon est supérieure à celle de la TNT
Variables d'effort et de flux
En général, on considère la puissance comme étant le produit d'une variable d'effort, qui est alors nécessaire à la mise en mouvement contre la résistance exercé par le système, par une variable de flux qui sera entretenue malgré l'existence de cette résistance
La variable d'effort peut correspondre à :
- Une force
- Un couple
- Une pression
- Une tension
La variable de flux peut correspondre à :
- Une vitesse
- Une vitesse angulaire
- Un débit
- L'intensité du courant
Afin d'illustrer ce propos, on peut prendre l'exemple de la puissance nécessaire afin d'imposer un déplacement à un véhicule.
En effet, cette puissance correspond alors au produit de la force de traction exercée par la vitesse de déplacement. De ce fait, la puissance d'un moteur rotatif correspond au produit du couple qu'il transmet au travers de la vitesse de rotation qu'il est capable d'entretenir malgré la résistance.
Autre exemple, l'ampoule électrique est capable de convertir l'énergie électrique en lumière et en chaleur.
Ainsi, la puissance consommée correspond au produit de la tension électrique par l'intensité du courant qui traverse cette ampoule. On peut définir la puissance moyenne Pm avec le quotient l'énergie E par la durée τ de ce phénomène :
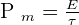
La puissance instantanée correspond quant à elle à la dérivée de l'énergie fournie par rapport au temps :
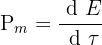
On obtient donc :
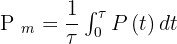
Le travail du poids

Cas de la chute libre d'un corps
On appelle chute libre le mouvement que prend un objet sous la seule action de son poids
Un tel mouvement ne peut avoir lieu que dans le vide. On peut admettre que dans l’air, la chute est "libre" si l’on peut négliger :
- Les frottements
- La poussée d’Archimède (il faut que la masse volumique de l’objet soit grande devant celle de l’air)
On a donc une variation du vecteur vitesse du centre d’inertie G de la bille :
- La valeur de la vitesse varie
- La direction reste constante.
On peut monter que pour une hauteur de chute h (en partant sans vitesse initiale), on a les deux relations suivantes ou v représente la vitesse :
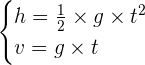
Un corps en chute libre n'est soumis qu'à la force de son poids. Le travail s'exprime alors de la manière suivante :

Lorsque que l'on passe aux norme des vecteurs, on a :

d'où 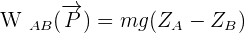
Nous voyons donc que pour un corps donné de masse m, le travail du poids ne dépend que de l'altitude.
La poussée d'Archimède
✅ La poussée d'Archimède est un phénomène physique qui décrit le comportement de tout corps plongé dans un fluide qu'il soit liquide ou gazeux soumis à un champ de gravité
Elle est nommée ainsi en l'honneur d'Archimède de Syracuse, un très grand scientifique grec de 200 avant J.-C.
Elle est causée par l'augmentation de la pression du fluide avec la profondeur. Comme la pression exercée sur la partie basse du corps est supérieure à celle exercée sur la partie haute, le corps est poussé verticalement vers le haut.
Voici la formulation d'origine de cette loi physique :
Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée poussée d'Archimède.
Pour que le théorème s'applique il faut que le fluide immergeant et le corps immergé soient au repos. Il faut également qu'il soit possible de remplacer le corps immergé par du fluide immergeant sans rompre l'équilibre.
Voici l'équation qui en résulte :
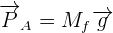
Avec :
- Mf< la masse du fluide contenu dans un volume V et déplacé ;
- g la valeur du champ de pesanteur, de 9,81 N/kg à la surface de la Terre.
Pour aller plus loin concernant la chute libre : chute libre sans vitesse initiale
L'accélération
La chute libre est un excellent exemple de mouvement rectiligne uniformément accéléré. En effet, chaque objet sur Terre est soumis à la force d'attraction gravitationnelle.
Un objet en chute libre est soumis, quelle que soit sa masse, à une accélération de pesanteur que l'on peut considérer constante au voisinage de la Terre.
En négligeant les forces de frottement, cette accélération est de direction verticale, orientée vers le bas et sa norme, appelée g est exprimée de la manière suivante :
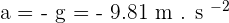 avec g la force gravitationnelle.
avec g la force gravitationnelle.
La vitesse
Nous avons démontré que la vitesse d'un mouvement rectiligne uniforme est de la forme :

d'où dans le cas d'une chute libre sans vitesse initiale, nous obtenons :
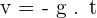 car vo est nulle
car vo est nulle
La position
Nous avons également l'expression de l'abscisse au cours du temps de la forme :
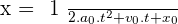
d'où dans le cas d'une chute libre sans vitesse initiale, nous obtenons : 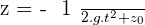 car vo est nulle et que le mouvement s'effectue le long de l'axe des ordonnées et non plus des abscisses.
car vo est nulle et que le mouvement s'effectue le long de l'axe des ordonnées et non plus des abscisses.
À noter que z peut aussi être appelé h (hauteur).
Paradoxe de la chute libre
Un caillou et une pierre de taille et de masses différentes lâchés en même temps sans vitesse initiale à 10 m de hauteur, frapperont le sol au même moment
En effet, en réalité les forces de frottement ne sont pas négligeables. Si la pierre, plus grosse et plus lourde devrait avoir une accélération plus importante, sa résistance à l'air est également bien supérieure à celle du cailloux. Ces deux forces se compensant, la pierre et le cailloux ont la même vitesse.
Cas d'un skieur glissant sur une piste

Prenons maintenant le cas, qui semble plus complexe, d'un skieur qui descend sans élan une piste de ski. Le poids de son corps et de ses équipements est donc la seul force exercée.
Ainsi, tel que vu plus haut, le poids est une force est conservative, et son travail ne dépend pas du chemin suivi. Seuls les positions de A et B comptent (cela dépend de la distance et de la pente).
Reprenons la définition du travail d'un poids :

De la même manière que pour la chute libre, exprimons le travail en fonction des normes des vecteurs :
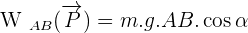
Exprimons alors le cos α en fonction des distances. Sur le schéma, le triangle vert est rectangle.
On peut donc écrire :

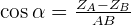
d'où 
soit 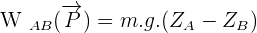
Soit la même expression que dans le cas de la chute libre.
Le travail du poids ne dépend donc que de la variation d'altitude.
Vous connaissez tout sur le travail de la force, et du poids ! Des questions ? Posez-les en commentaire.
Mais pour s’entraîner un peu, voici quelques exercices :
Si une personne pousse un chariot avec une force de 50 N sur 10 m dans la même direction que son déplacement. Quel est le travail effectué ?
Veuillez sélectionner une réponse.
Pour effectuer le calcul, il suffit d’appliquer la formule vue dans le cours :
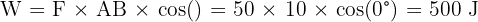
Une force est appliquée perpendiculairement au déplacement. Quel est donc le travail réalisé par cette force ?
Veuillez sélectionner une réponse.
Si la force est perpendiculaire au déplacement, alors cos(90°) = 0, donc le travail est nul.
La puissance mécanique est définie comme :
Veuillez sélectionner une réponse.
La puissance mécanique moyenne est : 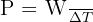
Imaginons qu’une force de 30 N est appliquée à un angle de 60° par rapport au déplacement sur 10 m. Quel est le travail ?
Veuillez sélectionner une réponse.
Pour trouver la solution, appliquer la formule suivante :
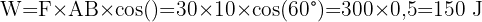
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Travail d’une force connaissant ses travaux sur les axes (OX) et (OY)
Bonjour, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! 🙂
Comment calculer la puissance si on connait la valeur de la vitesse, la longueur la masse d’un véhicule et on ne connait pas la valeur de la force??
Bonjour, nous serions ravis de vous aider ! Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique « Découvrir nos Superprofs » en indiquant la matière désirée. Vous trouverez de nombreux professeurs près de chez vous. 🙂
Comment peut-on exprimer w(f) en fonction de f, d et alpha ?
Bonjour, nous serions ravis de vous aider ! Avez-vous essayé de contacter l’un de nos professeurs ? Excellente journée ! :)
Bonjour, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! :)