Chapitres
- 01. Pour démarrer : notions sur la concentration massique
- 02. Théorie de la concentration massique
- 03. Calculer la concentration massique
- 04. En pratique : préparer une solution de concentration massique par dissolution ??
- 05. Les limites de la concentration massique ?
- 06. Tout savoir sur le processus de dilution ?
La concentration massique, également appelée concentration en masse ou densité de masse, est une mesure de la quantité de soluté dissous dans une solution. Elle est définie comme la masse du soluté par unité de volume de la solution. Elle s'exprime généralement en grammes par litre (g/L) ou en kilogrammes par mètre cube (kg/m³).
La concentration massique est couramment utilisée en chimie et en physique, notamment pour préparer des solutions, pour évaluer la pureté des produits chimiques ou pour mesurer la densité de matériaux solides. Elle peut être convertie en d'autres mesures de concentration telles que la concentration molaire en utilisant la masse molaire du soluté.
La concentration massique peut avoir des mises en pratique particulièrement utiles, par exemple :
Déterminer la teneur en sucre dans les boissons gazeuses
Mesurer la quantité de sel dans l'eau de mer

Pour démarrer : notions sur la concentration massique
Le volume
On utilise le mètre cube de symbole "m3". On utilise plutôt le litre en chimie (L).
1 m3 = 1000 L et 1 mL = 1 cm3
La masse volumique d'un échantillon est le rapport de la masse m de cet échantillon à son volume v. (ρ est la masse volumique)
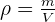
ou

ou
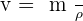
La densité d'un liquide est égale au quotient de la masse d'un volume v par la masse d'un même volume d'eau. (La densité s'exprime sans unité)
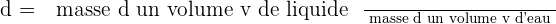
Définition du volume
Selon le domaine dans lequel ce mot est utilisé, la définition peut être différente. Mais, dans tous les cas, le volume représente une grandeur qui permet la mesure de l'extension d'un objet ou d'une partie de l'espace.
- En sciences physique, le volume d'un objet permet de mesurer l'extension dans l'espace physique que celui-ci possède et ce dans les trois directions de façon simultanée et de façon similaire à l'aire d'une figure dans le plan qui, quant à elle, mesure l'extension que celle-ci possède dans deux directions de façon simultanée.
- En mathématiques, le volume d'une partie de l'espace géométrique correspond à sa mesure dans le sens de la théorie de la mesure de Lebesgue.
Il peut être intéressant de connaître la notion de volume afin de déduire la masse d'un objet défini grâce notamment à la bien connue masse volumique !
La mole
La mole est une unité de quantité de matière. La quantité de matière se note "n" et s'exprime en mole de symbole mol.
Le nombre d'entités élémentaire contenue dans une mole est appelé Constante d'Avogadro, noté Na.
Il faut savoir que la valeur du nombre d'Avogadro a évolué au court du temps :
- Avant le 20 Mai 2019, le nombre d'Avogadro, et donc la mole, était défini comme correspondant au nombre d'atome de carbone dans 12 grammes (donc 10-3 kg) de carbone 12. On avait alors : NA = 6,022 140 857 . 1023 mol−1.
- Or, depuis le 20 Mai 2019, le kilogramme a été redéfini. Ainsi, on fit le choix de définir le nombre d'Avogadro comme étant une constante fixée par convention. Aujourd'hui, la valeur du nombre d'Avogadro est donc : NA = 6,022 140 76 . 1023 mol−1
Il y a proportionnalité entre le nombre N d'entités élémentaires dans un échantillon et sa quantité de matière n :
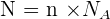
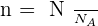
La masse
Petit rappel, ne pas confondre :
✅ La masse
Il s'agit d'une grandeur physique positive et intrinsèque d'un corps
❌ Le poids
Il dépend de la masse de l'objet et de l'intensité du champ gravitationnel
En effet, 100 ml d'eau aura la même masse, mais 100 ml d'huile aura une masse de 92,5 grammes

De façon plus précise, en physique newtonienne, la masse correspond à une grandeur extensive. Cela signifie alors que la masse d'un corps formé de parties correspond à la somme des masses de ces différentes parties qui le compose.
De plus, il est essentiel de noter que la masse est une grandeur conservative. De ce fait, elle reste constante dans le cas d'un système isolé qui n'échange donc pas de matière avec son environnement.
Pour une espèce donnée, la masse m, la quantité de matière n et la masse molaire M sont liés par :


Les propriétés
La masse peut se manifester au travers de deux propriétés fondamentales :
- 1️⃣ En mécanique statique, la masse est correspond à l'un des premières grandeurs facilement mesurables par les gens via le système de pesée puisque celle-ci permet de comparer la masse de l'objet défini avec un masse étalon connue. On appellera alors ce système la masse pesante. C'est ainsi que l'on liera la quantité de matière d'un corps à sa masse.
- 2️⃣ Tandis qu'en mécanique dynamique, la masse correspond à une grandeur qui intervient dans le principe fondamental de la dynamique comme étant la résistance de la matière au changement de vitesse. En effet, plus la masse d'un corps est importante, plus il faudra exercer une force importante pour modifier la direction ou encore sa vitesse. On appelle alors ce phénomène "masse inerte".
Ainsi, cet aspect de la masse présente un rôle essentiel dans tous les domaines de la dynamique puisqu'elle correspond à une notion présente dans grand nombre de relations de physique classique ou encore dans les calculs qui permettent de les définir.
En effet, il est possible de constater une proportionnalité entre la masse inerte et la masse pesante et cela de façon totalement indépendante de la nature du matériau mis en jeu. Cela permet alors de prendre la même unité pour la masse pesante et la masse inerte et donc de pouvoir les définir comme étant égale. Ainsi, cette équivalence a permis de définir un principe d'équivalence.
L'unité
L'unité de masse est le kilogramme dans le Système international d'unités (S.I.).
Comme pour le litre il existe des sous-unités : kg ; hg ; dag ; g ; dg ; cg ; mg.
❌ Attention à ne pas faire comme une majorité et confondre la masse avec le poids. En effet, dans le vocabulaire de la physique, le poids correspond à la force exercée par la gravité sur un corps pesant.
La masse molaire
La masse d'une mole d'atomes est appelée masse molaire atomique, noté M et d'unité g / mol. En chimie, on ne compte pas en nombre d'ions ou d'atomes mais en nombre de paquets, un paquet s'appelle une mole (mol). Une mole contient 6,02 . 1023 entités.
Le nombre de masse d’un atome correspond au nombre de nucléons qu’il contient. Il s’agit donc de la somme du nombre de protons et du nombre de protons qui constituent le noyau de l’atome.
La masse molaire correspond aussi au nombre de nucléons dans le noyau. A = 59, signifie qu'il y a 56 nucléons dans le noyau (et 59 grammes dans une mole).
Dans le tableau périodique, la masse molaire est souvent différente de A à cause des isotopes.
Des isotopes sont des atomes qui possèdent le même nombre de protons mais un nombre différent de neutrons.
Théorie de la concentration massique
La solution électrolytique
On appelle solution électrolytique toute solution obtenue par la dissolution d'une substance appelée soluté dans un liquide que l'on appelle solvant. Le soluté peut être sous la forme de solide, de gaz ou de liquide et si l'eau constitue le solvant de la solution, on parle alors de solution aqueuse.
De ce fait, une solution électrolytique correspond à une solution contenant des ions. Elle est alors conductrice tout en étant électriquement neutre
Créer une solution électrolytique par dissolution de cristaux ioniques
Détermination de la masse de soluté à peser
Soit à préparer un volume V d'une solution contenant l'espèce X, de masse molaire M(X), à la concentration [X]. Il faut, en général, déterminer la masse de l'espèce X à peser.
Soit m(X) cette masse.

or

Donc :

et

Le cristal ionique

Les cristaux ioniques sont constitués d'anions et de cations tenus entre eux par l'attraction électrique. Cette attraction est responsable de la structure géométrique qu'adoptent les ions pour former un cristal. Un ion positif va s'entourer d'ions négatifs et réciproquement et de la même manière que les atomes ou molécules forment les solides, les ions forment les cristaux.
✅ Exemple. Dans un cristal de chlorure de sodium NaCl, les ions adoptent une structure cubique où un anion est entouré de 6 cations. Un cristal ionique est toujours électriquement neutre donc il y a autant de charges positives que négatives. Par conséquent, certains cristaux possèdent plus d'anions et de cations (ou inversement).
Cohésion des cristaux ioniques
Les ions étant jointifs, la distance qui les sépare correspond à la distance entre leur centre.
La cohésion du cristal est due à l'interaction coulombienne qui correspond à la force qui lie deux ions. La valeur de cette force peut paraître faible mais elle est bien plus importante par rapport au poids de l'ion. A cette échelle, c'est la force électrique qui domine. La température de fusion des solides ioniques est assez élevée (801 °C) pour le sel, ce qui veut dire que les liaisons entre ions sont très solides.
La loi de Coulomb
Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés. Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposée et répulsive sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie donc en raison inverse du carré de la distance r.
Il est alors possible de traduire ces caractéristiques en une formule exprimant la force exercée par q1 sur q2 :

Avec :
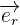 le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2
le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2 la permittivité diélectrique du vide
la permittivité diélectrique du vide
Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance. En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare.
Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force et donc d'obtenir la relation suivante :
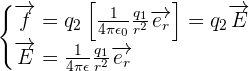
Avec :
 un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance. En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique. Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Calculer la concentration massique
La concentration massique est une grandeur qui reflète la proportion de soluté dissout dans une solution aqueuse.
On la note communément Cm mais le Bureau International des poids et mesures (BIPM) préconise d’utiliser davantage ρi ou γi.
Note : Ici, nous nous contenterons de la notation usuelle, à savoir Cm
La concentration massique se calcule en divisant la masse de soluté (m) par le volume de la solution (V) ce qui peut se traduire par la relation suivante :
Cm = m/V
- m en gramme ( g )
- V en litre ( L)
- Cm en gramme par litre (g.L-1)
?? Par exemple, on dissout 5 g de sulfate de cuivre dans 400 mL d’eau. Quelle est alors la concentration massique du sulfate de cuivre ?
- On a : m = 5g, V= 400 mL
- Il faut, dans un premier temps convertir en litres le volume d’eau V. Ainsi, V = 400 mL = 0,4 L
- On peut donc écrire : Cm = 5/o,4
- Ainsi : Cm = 12,5 g.L-1
La concentration massique du sulfate de cuivre est de 12,5 g.L-1.
Remarque : Comme pour toute autre concentration, il est possible d’exprimer la concentration massique avec d’autres unités. Il est néanmoins impératif de veiller à utiliser des unités de masses et de volumes qui restent cohérentes.
Par exemple pour une concentration massique en milligramme par litre (mg/L) alors la masse doit être exprimée en milligramme (mg) et le volume en litre (L). C’est logique ! Mais il est facile de faire des erreurs d’unités alors il faut faire attention.
Calculer une masse à partir de la concentration massique
Pour calculer une masse, on revient à la relation précédente qui permettait de calculer la concentration massique et on a :
m = Cm x V
- m en gramme (g)
- V en litre (L)
- Cm en gramme par litre (g.L-1)
Prenons une solution de concentration massique Cm =15 g.L-1 et de volume V = 3 L. Quelle est alors la masse de la solution ?
- On sait que : m = Cm x V
- D’où : m = 15 x 3
- Donc : m = 45 g
La masse de la solution est donc de 45 g.
Calculer le volume de solution contenant une masse m de soluté
Tout comme pour le calcul de masse il suffit de modifier l’expression de la concentration massique:
V = m/Cm
- m en gramme (g)
- V en litre (L)
- Cm en gramme par litre (g.L-1)
On a une solution de concentration massique de 2,5 g.L-1. De plus, le volume de solution renferme 0,5 g de soluté. Quelle est donc le volume de solution présent ?
On sait que : V = m/Cm
- m en gramme (g)
- V en litre (L)
- Cm en gramme par litre (g.L-1)
Donc : V = 0,5/2,5
Ainsi, V = 0,2 L.
Le volume de solution présent est de 0,2L.
Somme des concentrations massiques et masse volumique
Il existe également une relation entre la concentration massique et la masse volumique.
Prenons une solution qui est composée de plusieurs espèces chimiques et nous sommes amenés à additionner les concentrations massiques des différents composants de cette solution. Cette somme des concentrations massiques est en fait égale à la masse volumique de la solution.
On peut alors écrire :
ρ = (Cm)
Explications (voir aussi la fiche sur la masse volumique)
Comme Cm = m/V on a :
Cm = (m)/V = M/V = ρ
Concentration massique et concentration molaire
Concentration massique et concentration molaire sont également deux grandeurs liées par la relation suivante :
Cm = C * M où C est la concentration molaire et M la masse molaire d’une solution
Comment peut-on expliquer cela mathématiquement ?
Il suffit de reprendre toutes les relations que nous connaissons liées à la concentration molaire, la masse molaire, la masse et la quantité de matière.
- On sait en effet que : m = n * M
- On sait aussi que : C = n/V
Ainsi on peut remplacer m dans notre relation de base par n * M et on a alors :
- Cm = m/V = (n*M)/V = (n/V)*M
- Comme C = n/V, on peut donc écrire : Cm = C * M.
En pratique : préparer une solution de concentration massique par dissolution ??
Comprendre ce que l'on fait
⚠️ Il faut être attentif aux notions que l’on utilise et savoir faire la distinction entre ces trois termes extrêmement liés et souvent sujets à confusion :
Solvant
Soluté
Solution
En fait, la solution est le résultat de la dissolution d’une espèce chimique quelconque dans un solvant. Cette espèce, une fois dissoute, est appelée soluté.
En d’autres termes, le solvant est le liquide dans lequel se dissout le soluté. Ce dernier peut, quant à lui, prendre toutes les formes physiques : liquide, gazeuse ou solide.
Le solvant très souvent utilisé en laboratoire est l’eau. On parle alors de solution aqueuse.
Le matériel indispensable pour préparer une solution de concentration massique

- Balance
- Spatule
- Capsule
- Fiole jaugée de volume V
- Eau distillée
Le protocole à mettre en place
En laboratoire, il est possible de préparer une solution d’un volume V donné et une concentration massique Cm donnée. Ainsi, il s’agit là d’une dissolution !
- Pour ce faire, il faut, dans un premier temps calculer la masse de soluté nécessaire à la préparation. On utilise alors la relation suivante : m = Cm x V.
- On mesure ainsi la masse calculée à l’aide d’une balance. Pour cela, on utilise une spatule propre et sèche et on prend délicatement du soluté que l’on verse ensuite dans une capsule. Attention à peser cette capsule préalablement et à tarer.
- On verse ensuite la quantité de soluté mesuré dans une fiole jaugée au volume V donné.
- On ajoute de l’eau distillée aux deux-tiers. On bouche la fiole jaugée et on agite.
- On complète enfin jusqu’au trait de jauge sans oublier de d’agiter à nouveau pour que le soluté soit complètement dissous.
Les limites de la concentration massique ?
La concentration massique ne prend pas en compte la taille ou la forme des particules du soluté. Cela peut être un problème car des particules plus grandes ou de formes différentes peuvent avoir une solubilité différente dans le solvant, ce qui affecte la concentration.
De plus, la concentration massique ne prend pas en compte les interactions intermoléculaires entre le solvant et le soluté. Ces interactions peuvent affecter la solubilité d'un composé et donc sa concentration dans la solution.
Dans certains cas, il peut être plus approprié d'utiliser d'autres mesures de concentration pour tenir compte de ces limites.
✅ Par exemple, pour les solutés qui ne se dissolvent pas facilement ou pour les solutions diluées, la concentration molaire peut être plus appropriée car elle mesure la quantité de soluté par rapport au volume total de la solution.
✅ De même, la concentration pondérale peut être utilisée pour mesurer la masse du soluté par rapport à la masse totale de la solution. Cette mesure peut être plus appropriée pour les solutions très concentrées ou pour les solutés de faible masse moléculaire.
Tout savoir sur le processus de dilution ?
La dilution correspond à un procédé qui consiste en l'obtention d'une solution finale qui présentera une concentration inférieure à la concentration de la solution de départ.
Il est alors possible de procéder à cela grâce à un ajout de solvant ou encore en prélevant une partie de la solution puis de compléter jusqu'à atteindre le volume souhaité avec du solvant. Il est alors possible de caractériser une dilution par son taux de dilution.
Mais pour cela, il est nécessaire de présupposer que le corps dilué est soluble dans le solvant qui est utilisé.
Dilution par ajout de solvant
On note la concentration d'une solution C et il est possible de la calculer avec la formule suivante :

Avec :
- C la concentration molaire. Cette unité s'exprime en mol.L-1 ;
- n la quantité de matière du soluté en solution. Cette unité s'exprime en mol ;
- Et V le volume de solvant. Cette unité s'exprime en L.
Ainsi, si on procède à une dilution par ajout de solvant, la solution initiale et la solution finale contiennent autant de quantité de soluté. Cela signifie alors que ninitiale = nfinale .
On a alors les relations suivantes qui se dégagent :
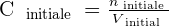

On peut déduire de ces relations le rapport suivant :
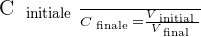
Qu'est-ce que le taux de dilution ?
Il est possible d'exprimer le taux de dilution avec la relation suivante :
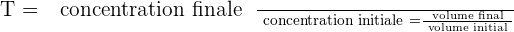
Il est important de savoir que le taux de dilution, noté T, est une grandeur sans unité et qui présente obligatoirement une valeur positive et inférieure à 1.
Quant au taux de dilutions successives, il correspond au produit des taux de dilution de chaque dilution.
Exemple
Si on procède à une dilution à 3 % puis à 5 %, on a T qui est égal à :

Lien entre l'homéopathie et la dilution

L'homéopathie correspond à une pratique pseudo-scientifique de médecine alternative qui a été inventée en 1796 par Samuel Hahnemann
Cette pratique repose essentiellement sur le principe qu'il est possible de soigner un patient en diluant très fortement des substances qui, lorsqu'elles sont concentrées, pourraient provoquer des symptômes assez similaires à ceux que le patient rencontre.
Or, au-delà d'un certain nombre de dilutions, les remèdes se basant sur l'homéopathie sont totalement dépourvus de tout principes actifs.
Afin de mettre au point un remède homéopathique, il est nécessaire d'utiliser la technique de dilutions infinitésimales. Ce principe consiste à diminuer la toxicité des substances choisies dans la composition du remède par application du principe de similitude. Par suite de cela, il est nécessaire d'agiter très fortement les préparations. Ainsi, après chaque dilution, la préparation est secouée de façon énergique manuellement ou mécaniquement.
Cela permettrait de conserver les effets pharmacologiques du principe malgré des dilutions importantes.
Le mécanisme de la mémoire de l'eau
Pour expliquer cette méthode, Jacques Benveniste, en 1987, mettra au point l'hypothèse de la mémoire de l'eau. Cette hypothèse reposerait sur la possibilité que l'eau garderait en mémoire les propriétés de la substances précédemment diluées même lorsque ces substances sont absente sous la forme d'une empreinte électromagnétique de la molécule.
Cependant, cette hypothèse est considérée comme scientifiquement invraisemblable, et les précédentes démonstrations de cette hypothèse ne furent nullement convaincantes car truquées ou biaisées par la présence d'artefacts de manipulations.
La dilution utilisée lors des dosages colorimétriques
Un dosage colorimétrique correspond à un type de dosage qu'il est possible de réaliser lorsqu'une réaction chimique donne des produits colorés et si l'intensité de la coloration est proportionnelle à la concentration de l'élément chimique à doser. Cette réaction repose donc logiquement sur la loi de Beer-Lambert.
Notez qu'il est aussi possible de procéder à un dosage colorimétrique en utilisant des indicateurs colorés qui vont se colorer selon les variations de pH et donc indiquer le point d'équivalence de la réaction. Dans ce cas, on parle alors de titrage colorimétrique.
Pour procéder à un tel dosage, il est alors nécessaire de procéder à la conception d'une gamme étalon.
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bien. Concentration massique Cm.m/v. m.cm×v. V.m/cm
bonjour,
le calcul de la concentration massique par dilution et dissolution est t’il le meme ?
Bonjour Naya,
La dissolution et la dilution sont deux procédés qui fonctionnent différemment. Vous pourrez trouver toutes les informations qu’il vous faut concernant la dilution ici.
Pour ce qui est de la dissolution, il y a plusieurs facteurs à prendre comme la température, la concentration de la solution et la masse à dissoudre par exemple.
Quelle est la masse utilisée pour préparer 1L de solution de sulfate de fer de concentration 0.0004 mol/ml. Si l’un des sels suivant est utilisé:
1) sulfate de fer anhydre (FeSO4).
2) sulfate de fer 7 fois hydraté (FeSO4,7H2O).
3)sulfate de fer livré avec un taux de pureté égale à 40%.
Données: M(Fe)=56g/mol ; M(S)=32g/mo; M(O)=16g/mo;M(H)=1g/mol.
Bonjour Tayma,
Désolée nous pouvons vous donner les clefs pour résoudre vos problèmes via les cours que nous mettons à disposition mais si vous souhaitez une aide plus active concernant les exercices, vous pouvez toujours vous tourner vers un de nos professeur. (Pour apprendre, il vaut mieux faire soit même plutôt que de donner directement la réponse ;) )
J’adore ce siteee !!! La BEST chose pour comprendre le cours !
Youpi
J’ai un petit problème:
J’ai une solution A concentrée à 1,4%
J’ai une solution B concentrée à 8,4%
Quel volume de B dois-je ajouter dans A pour avoir une solution concentrée à 6,4% svp?