Chapitres

Le champ magnétique
Champ électrique
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance.
Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi :
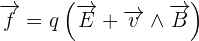
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude.
Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes.
Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb.
On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet.

Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électromagnétique
En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante :
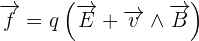
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
 le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude.
De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante.
D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique.
La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Comportement des aimants
Des aimants peuvent s'attirer ou se repousser selon la face que l'on présente l'un à l'autre.
Un aimant possède deux pôles : nord et sud, deux pôles identiques se repoussent et deux pôles opposés s'attirent.
Seuls les matériaux contenant du fer ont des propriétés magnétiques.
Définition d'un champ
Un champ décrit une région de l'espace dans laquelle une source engendre sur un objet physique une action. Chaque point de la région concernée possède une valeur numérique ou vectorielle attribuée à la grandeur physique qui décrit le champ.
Si les points de l'espace portent une valeur numérique, le champ est dit scalaire (temps), s'ils portent un vecteur, le champ est dit vectoriel.
Champ B
En un point de l'espace M autour d'une source magnétique, on peut définir le champ magnétique de B en M. Les caractéristiques sont les suivantes :
- Sa direction est indiquée par l'aiguille d'une boussole aimantée
- Son sens est toujours du nord vers le sud de la source
- L'intensité (unité Tesla), elle diminue quand on s'éloigne de la source
Lignes de champ
Les lignes tangentes au vecteur B en tout point de l'espace se nomment lignes de champ.
Elles sont orientées comme le champ B du nord vers le sud de la source et l'ensemble de ces lignes se nomme le spectre magnétique de la source.
Le champ magnétique
Distribution de courant filiforme
- L'intensité électrique est adaptée pour décrire une répartition de courants localisée dans un tube de faible section (cas des fils électriques), tube qui sera "vu" de loin comme un fil dont on néglige l'épaisseur,
- Définition de l'intensité électrique.
Invariances par translation et rotation
- Si une distribution de courants est invariante par translation dans une direction donnée, le champ magnétique créé sera également invariant dans cette direction,
- Si une distribution de courants est invariante par rotation autour d'un axe, la norme du champ magnétique créé sera également invariante par rotation.
Propriétés du champ magnétique en tout point d'un plan de symétrie ou d'un plan d'antisymétrie des courants
Définitions
- Un plan de symétrie d'une distribution de courants est un plan qui laisse invariante cette distribution de courants lorsqu'on effectue la symétrie plane,
- Un plan d'antisymétrie d'une distribution de courants est un plan qui laisse invariante cette distribution de courants mais en inversant les sens des courants lorsqu'on effectue la symétrie plane.
Propriétés
- En un point appartenant à un plan de symétrie d'une distribution de courants, le champ magnétostatique est orthogonal à ce plan. (Admis)
- En un point appartenant à un plan d'antisymétrie d'une distribution de courants, le champ magnétostatique appartient à ce plan. (Admis)
- Les propriétés pour les champs électrostatiques et magnétiques diffèrent : E est un "vrai" vecteur alors que B est un "pseudo" vecteur car défini à partir d'une convention mathématique d'orientation (celle du produit vectoriel).
Plans de symétrie ou d’antisymétrie des courants
Un plan est un plan de symétrie des sources du champ si elles restent inchangées lorsqu'on effectue la symétrie par rapport à ce plan.
Un plan est un plan d'antisymétrie des sources du champ si elles sont inversées (changement de signe pour les charges, de sens pour les courants) lorsqu'on effectue la symétrie par rapport à ce plan.
En tout point d'un plan de symétrie des sources, le champ électrique est contenu dans ce plan et le champ magnétique est orthogonal à ce plan.
En tout point d'un plan d'antisymétrie des sources, le champ magnétique est contenu dans ce plan et le champ électrique est orthogonal à ce plan.
Calculer un champ magnétique
Les méthodes sont numérotées par ordre de priorité.
Lorsqu'une action proposée est impossible, passer à la méthode suivante.
Méthode 1 : Théorème de superposition.
- Décomposer la distribution de courant en quelques distributions simples,
- Pour chaque distribution, calculer le champ magnétique au point M considéré en utilisant éventuellement les méthodes qui suivent,
- Additionner les champs en indiquant qu'il s'agit du théorème de superposition.
Attention :
- Les champs s'ajoutent en un même point M de l'espace,
- Il s'agit d'une somme vectorielle.
Rappel : somme vectorielle
Méthode 1 :
Utiliser la relation de Chasles en utilisant une notation intrinsèque pour les champs.
Méthode 2 :
- Déterminer la direction du champ total au point M :
- Méthode 1 : associer deux par deux des champs symétriques,
- Méthode 2 : trouver un plan de symétrie ou deux plans d'antisymétrie de la distribution de courants passant par M.
- Projeter les champs à additionner dans cette direction,
- Sommer ces différentes projections :
- Méthode 3 : Faire la somme des composantes dans une base orthonormée bien choisie,
- Méthode 4 : Somme graphique.
Méthode 2 : Théorème d'Ampère
- Déterminer l'allure du spectre dans tous l'espace d'étude :
- Déterminer la direction du champ en un point M quelconque de l'espace :
- Méthode 1 : associer deux par deux des champs élémentaires symétriques,
- Méthode 2 : trouver un plan de symétrie ou deux plans d'antisymétrie de la distribution de courants, passant par M.
- Déterminer les variables dont dépend la norme du champ dans l'espace, en évoquant des arguments d'invariance par translation ou rotation du problème vu par l'observateur,
- Choisir un contour d'Ampère passant par le point où on cherche le champ : Pour simplifier le calcul de la circulation, le contour doit suivre les lignes de champ ou les couper orthogonalement,
- Appliquer le théorème d'Ampère.
Superposition de champs
Principe de superposition
Il est possible d'appliquer le principe de superposition à un système de type entrée-sortie si :
- La somme de deux entrées quelconque correspond à la somme des deux sorties correspondantes ;
- Un multiple d'une entrée quelconque correspond le même multiple de la sortie correspondante.
Dans ce cas, c'est-à-dire celui d'un système physique, on peut appeler l'entrée excitation et la sortie réponse.
On obtient alors, en notant les excitations ƒ et les réponses x (donc les mouvements généré par les forces mécaniques ƒ) :
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ1, une réponse, donc un déplacement, qui sera noté x1 ;
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ2, une réponse, donc un déplacement, qui sera noté x2 .
Champ uniforme
Un champ est uniforme lorsque ses lignes de champ sont parallèles et il a la même valeur en tout point. C'est le cas par exemple dans un aimant en U
Superposition de champ
La superposition de deux champs magnétiques crée un champ unique représentée par un vecteur égal à la somme vectorielle des deux champs superposés.
Le théorème de Gauss
Le théorème de Gauss permet, en électromagnétisme, de calculer le flux d'un champ électrique à travers une surface qui est fermée et ce grâce à la connaissance des charges électriques que cette surface renferme.

Il s'énonce ainsi :
Le flux du champ électrique à travers une surface S fermée est égal à la somme des charges électriques contenues dans le volume V délimité par cette surface, divisée par la permittivité du vide.
Loi de Coulomb
Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés. Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposée et répulsive sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie en raison inverse du carré de la distance r.
Il est alors possible de traduire ces caractéristiques en une formule exprimant la force exercée par q1 sur q2 :

avec :
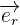 le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2
le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2 la permittivité diélectrique du vide
la permittivité diélectrique du vide
Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance. En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare.
Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force et donc d'obtenir la relation suivante :
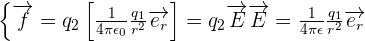
avec :
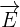 un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance. En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique. Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Equations locales de l'électromagnétisme
1. But de l'électromagnétisme
- But de l'électromagnétisme : Décrire l'action d'une distribution de charges sur une autre.
- Utilisation d'un intermédiaire qu'est le champ électromagnétique. Il faut donc savoir
- déterminer le champ créé par une distribution de charges
- déterminer l'action subie par l'autre distribution dans ce champ.
- Le champ électromagnétique n'est pas un simple intermédiaire de calcul. C'est une entité physique à part entière comme le montre l'étude des phénomènes de propagation.
a. Description d'une distribution de charges.
- Densité volumique de charge.
- Densité volumique de courant.
b. Champ électromagnétique créé par une distribution de charges : Equations de Maxwell
- Quatre équations de Maxwell qui relient les champs électromagnétiques aux charges.
- Les équations de Maxwell sont linéaires : on a donc le théorème de superposition des solutions.
- En régime quelconque, les équations de Maxwell sont couplées : le champ électromagnétique forme un tout indissociable.
c. Actions subies par une distribution de charges.
- Par une charge ponctuelle : force de Lorentz.
- Par une distribution volumique de charges : force volumique de Lorentz.
- Par un conducteur parcouru par un courant : force de Laplace.
- Interprétation de l'origine de la force de Laplace.
- Règle du flux maximum (admise) : les forces de Laplace sur un circuit fermé tendent à rendre le flux du champ magnétique maximal à travers le circuit.
- Par un dipôle électrique : expression de la résultante et du moment résultant.
- action principale: tendance à l'alignement dans le champ électrique.
- action secondaire: tendance à se déplacer vers les zones de champ fort.
- Par un dipôle magnétique: expression de la résultante et du moment résultant.
- action principale: tendance à l'alignement dans le champ magnétique.
- action secondaire: tendance à se déplacer vers les zones de champ fort.
2. Symétries du champ électromagnétique.
- Un plan est un plan de symétrie d'un problème si les sources du champ restent inchangées lorsqu'on effectue la symétrie par rapport à ce plan.
- Un plan est un plan d' antisymétrie d'un problème si les sources du champ sont inversées (changement de signe pour les charges, de sens pour les courants) lorsqu'on effectue la symétrie par rapport à ce plan.
- Le champ électrique est un "vrai" vecteur donc
- en tout point d'un plan de symétrie des sources, le champ électrique est contenu dans ce plan,
- en tout point d'un plan d' antisymétrie des sources, le champ électrique est orthogonal à ce plan.
- Le champ magnétique est un "pseudovecteur" (sa définition inclut la convention arbitraire d'orientation du produit vectoriel) donc
- en tout point d'un plan de symétrie des sources, le champ magnétique est orthogonal à ce plan,
- en tout point d'un plan d' antisymétrie des sources, le champ magnétique est contenu dans ce plan.
3. Equation locale de conservation de la charge
a. Intensité électrique
- Par définition, c'est un débit de charge algébrique à travers une surface orientée.
- Par le calcul, on obtient le flux du vecteur densité de courant à travers cette surface. L'intensité dépend donc de la surface.
b. Bilan de conservation de la charge
- Formulation intégrale.
- Equation locale de conservation de la charge.
c. Démonstration de l'équation locale de conservation de la charge à partir des équations de Maxwell.
- La rapidité de cette démonstration mathématique se fait au détriment de la compréhension physique.
4. Contenu physique des équations de Maxwell
a. Equation de Maxwell- Gauss
- Théorème de Gauss.
- Conséquences :
- Le champ électrique est à flux conservatif en dehors des charges : le champ augmente donc quand les lignes de champ se ressèrent.
- En un point d'où divergent ou convergent les lignes de champ électrique se trouve une charge.
b. Equation de Maxwell- Ampère
- Théorème d'Ampère généralisé.
c. Equation du flux magnétique
- Les lignes de champ ne peuvent ni converger en un point, ni diverger d'un point.
- Le champ magnétique est à flux conservatif : le champ augmente donc quand les lignes de champ se ressèrent, et on peut définir le flux du champ magnétique à travers un contour.
d. Equation de Maxwell - Faraday
- Loi de Faraday.
5. Résolution des équations de Maxwell
a. Utilisation des potentiels
- Introduction du potentiel scalaire électrique et du potentiel vecteur magnétique.
- L'introduction des potentiels a pour but de découpler les équations de Maxwell. (Démonstration hors programme)
b. Non unicité des potentiels
- Le choix du couple (potentiel scalaire électrique - potentiel vecteur magnétique) n'est pas unique.
- On peut imposer une condition supplémentaire entre ces deux potentiels : on utilise la jauge de Lorentz. (Hors programme)
- Les deux potentiels vérifient alors des équations du même type découplées : équation d'onde.
- La solution des potentiels retardés (hors programme) montre que les champs ne se propagent pas de façon instantanée des sources au point d'observation. Ils se propagent à la vitesse c dans le vide.
6. Relations de passage
a. Discontinuité du champ électrique
- En présence de répartitions volumiques de charges dans l'espace, le champ électrique et son potentiel sont continus dans tout l'espace.
- Les discontinuités éventuelles sont dues aux modélisations mathématiques des répartitions de charges.
- Rappels : modélisations surfaciques et linéiques de répartitions de charges.
- Les discontinuités éventuelles du champ électrique et de son potentiel n'existent qu'au niveau de ces répartitions de charges modélisées.
- Pour une répartition surfacique de charges :
- le champ électrique est discontinu à la traversée de cette surface,
- le potentiel électrique est continu.
- Pour une répartition linéique de charges :
- le champ électrique est discontinu,
- le potentiel est discontinu.
- Relations de passage du champ électrique à la traversée d'une surface chargée (admises) :
- la composante tangentielle du champ électrique est continue.
- la composante normale du champ électrique est discontinue.
- les relations de passage remplacent les équations de Maxwell-Gauss et Maxwell-Faraday sur la surface.
b. Discontinuité du champ magnétique
- En présence de répartitions volumiques de courants dans l'espace, le champ magnétique et son potentiel vecteur sont continus dans tout l'espace.
- Les discontinuités éventuelles sont dûes aux modélisations mathématiques des répartitions de courant.
- Rappels : modélisations surfaciques et linéiques de répartitions de courants.
- Les discontinuités éventuelles du champ magnétique et de son potentiel vecteur n'existent qu'au niveau de ces répartitions de courants modélisées.
- Pour une répartition surfacique de courants :
- le champ magnétique est discontinu à la traversée de cette surface,
- le potentiel vecteur magnétique est continu.
- Pour une répartition linéique de courants :
- le champ magnétique est discontinu,
- le potentiel vecteur est discontinu.
- Relations de passage du champ magnétique à la traversée d'une répartition surfacique de courants (admises) :
- la composante tangentielle du champ magnétique est discontinue.
- la composante normale du champ magnétique est continue.
- les relations de passage remplacent les équations de Maxwell-ampère et Maxwell-flux sur la surface.
7. Aspect énergétique : équation locale de Poynting
a. Démonstration à partir des équations de Maxwell
- Définition du vecteur de Poynting
- Équation locale
b. Signification physique
- Loi de Joule microscopique : expression de la puissance volumique fournie par un champ électromagnétique à des porteurs de charge libres : en retenant que la force magnétique ne travaille pas, que la force électrique est proportionnelle à la charge et que la puissance reçue dépend de la vitesse, il est clair que l' expression de la puissance va faire intervenir le champ électrique et le vecteur densité de courant.
- Remarque : Passage à la loi de Joule macroscopique pour une portion de circuit en régime permanent.
- Densité volumique d'énergie électromagnétique : on admet que chaque élément de volume de l'espace contient une énergie potentielle (donc récupérable) de par la présence d'un champ électrique et d'un champ magnétique.
- Vecteur de Poynting : on admet que la direction du vecteur de Poynting donne la direction de propagation de l'énergie électromagnétique, et que le flux du vecteur de Poynting à travers une surface représente le débit d'énergie à travers cette surface, c'est à dire l'énergie qui traverse la surface par unité de temps, c'est à dire aussi la puissance qui traverse la surface.
- Bilan énergétique : il redonne l'équation locale de Poynting.
8. Cas particulier du régime statique
a. Simplification des équations
- Ce sont les charges qui créent le champ qui sont statiques, pas celles qui le subissent.
- Equations de Maxwell :
- Seul le champ électrique existe (on le nomme champ électrostatique).
- Seul le potentiel électrique existe (on le nomme potentiel électrostatique)
- Topographie du champ électrostatique :
- Les lignes de champ sont normales aux surfaces équipotentielles.
- Les lignes de champ peuvent diverger d'un point : il y a alors une charge ponctuelle positive en ce point.
- Les lignes de champ peuvent converger vers un point : il y a alors une charge ponctuelle négative en ce point.
- Il n'existe donc pas d' extremum du potentiel en dehors des charges puisque le potentiel décroit le long d'une ligne de champ.
- En dehors des charges, le champ augmente quand les lignes de champ se ressèrent.
- Les lignes de champ ne se referment pas sur elles-même.
- Relations de passage : ce sont les mêmes que dans le cas général.
- Résolution des équations de Maxwell :
- Utilisation du potentiel.
- Equation de Poisson.
- Solution en l'absence de charges à l'infini et en prenant le potentiel nul à l'infini.
- Retour au champ électrique : loi de Coulomb.
b. Exemples de calculs de champs électrostatiques
- Dans l'ordre des méthodes à utiliser :
- Principe de superposition.
- Théorème de Gauss quand les symétries sont suffisantes, ou directement l'équation de Maxwell-Gauss en distribution volumique.
- Loi de Coulomb : intégrale vectorielle donc trois intégrales scalaires à priori sauf si on détermine au préalable la direction du champ.
- Passage par le potentiel : une seule intégrale scalaire mais il faut faire très proprement le passage au champ.
- Cas particulier du champ créé par un dipôle électrique :
- Expression du potentiel électrique.
- Passage au champ électrique dans la base de coordonnnées sphériques.
- Expression intrinsèque du champ électrique créé.
9. Cas particulier du régime stationnaire
a. Simplification des équations
- Les charges qui créent le champ sont en mouvement mais de façon stationnaire : le vecteur densité de courant est non nul mais indépendant du temps, les champs sont indépendants du temps.
- Equation locale de conservation de la charge :
- Le vecteur densité de courant est à flux conservatif donc le courant est identique en tout point d'un fil.
- Loi des noeuds .
- On peut définir l'intensité à travers un contour.
- Equations de Maxwell :
- Les deux champs électrique et magnétique existent mais sont découplés.
- La détermination du champ électrique à partir des charges est identique au cas de l'électrostatique.
- Le champ magnétique est nommé champ magnétostatique.
- Théorème d'Ampère : on peut définir le courant qui traverse un contour.
- Topographie du champ magnétique :
- Les lignes de champ peuvent se refermer sur elles-même : elles enlacent alors des courants et leur orientation est donnée par la règle du tire-bouchon.
- Les lignes de champ ne peuvent ni converger en un point, ni diverger d'un point.
- Le champ magnétique est à flux conservatif : le champ augmente donc quand les lignes de champ se ressèrent.
- Relations de passage : les mêmes que dans le cas général.
- Résolution des équations de Maxwell pour le champ magnétique :
- Introduction du potentiel vecteur.
- Jauge de Coulomb.
- Equation de Poisson pour le potentiel vecteur.
- Solution en l'absence de courants à l'infini et en prenant le potentiel nul à l'infini. (Son utilisation est hors programme)
- Conséquence : le potentiel vecteur est un vrai vecteur.
- Passage au champ magnétique : loi de Biot et Savart.
b. Exemples de calculs de champ magnétostatique
- Dans l'ordre des méthodes à utiliser :
- Principe de superposition.
- Théorème d'Ampère quand les symétries sont suffisantes, ou directement l'équation de Maxwell-Ampère pour des distributions volumiques.
- Loi de Biot et Savart : intégrale vectorielle donc trois intégrales scalaires à priori sauf si on détermine au préalable la direction du champ.
- Passage par le potentiel vecteur : intégrale vectorielle également donc pas plus simple (et hors programme).
- Cas particulier du champ magnétique créé par un dipôle magnétique :
- Champ magnétique dans la base de coordonnées sphériques, par analogie au cas électrique.
- Expression intrinsèque du champ magnétique créé.
c. Exemples de calcul de potentiel vecteur à partir du champ magnétique
- Peut servir pour calculer un flux, un champ électromoteur.
- Potentiel vecteur créé par un fil infini.
- Potentiel vecteur d'un champ uniforme : expression donnée, à vérifier.
10. Cas particulier des régimes lentement variables. Approximation des régimes quasi stationnaires (ARQS)
a. Définition de l'approximation
- l' ARQS consiste à négliger la propagation des champs électromagnétiques dans la portion d'espace étudiée.
En régime sinusoïdal, les variations spatiales des champs dues à la propagation ont pour période la longueur d'onde. Il suffit donc que la dimension de l'espace d'étude soit très inférieure à la longueur d'onde.
- Dans les équations de Maxwell, il suffira de faire tendre c vers l'infini, donc εoμo vers 0.
- Dans la suite de ce cours, on se placera dans l'approximation des régimes quasistationnaires.
b. Conséquences
- Equations de Maxwell :
- Les deux champs électrique et magnétique existent et sont couplés.
- La détermination du champ magnétique à partir des courants est identique au cas de la magnétostatique car l'approximation revient à négliger le terme de courant de déplacement.
- Attention : le champ électrique ne se calcule plus comme le champ électrostatique : les variations temporelles de champ magnétique sont sources de champ électrique (phénomène d'induction).
- Equation locale de conservation de la charge :
- Le vecteur densité de courant est à flux conservatif donc le courant est identique en tout point d'un fil.
- Loi des noeuds.
- On peut définir l'intensité à travers un contour.
- Relations de passage : les mêmes que dans le cas général.
- Résolution des équations de Maxwell :
- Utilisation des potentiels.
- Equations de Poisson pour les potentiels.
- Solution en l'absence de courants à l'infini et en prenant les potentiels nuls à l'infini
Couplage entre les champs électrique et magnétique dans l'ARQS
1. Mise en évidence expérimentale du phénomène
a. Interaction entre un aimant et une spire
- Lorsque l'aimant est en mouvement vers la spire, il y a apparition d'un courant dit "induit" dans la spire. Le sens de ce courant induit a pour effet de faire apparaître une force répulsive entre l'aimant et la spire, force qui s'oppose donc au mouvement de l'aimant.
- Lorsque l'aimant est en mouvement en s'éloignant de la spire, il y a apparition d'un courant dit "induit" dans la spire. Le sens de ce courant induit a pour effet de faire apparaître une force attractive entre l'aimant et la spire, force qui s'oppose donc au mouvement de l'aimant.
- Lorsque la spire est en mouvement vers l'aimant, il y a apparition d'un courant dit "induit" dans la spire. Le sens de ce courant induit a pour effet de faire apparaître une force répulsive entre l'aimant et la spire, force qui s'oppose donc au mouvement de la spire.
- Lorsque la spire est en mouvement en s'éloignant de l'aimant, il y a apparition d'un courant dit "induit" dans la spire. Le sens de ce courant induit a pour effet de faire apparaître une force attractive entre l'aimant et la spire, force qui s'oppose donc au mouvement de la spire.
b. loi de Lenz (1834)
- Les effets du courant induit s'opposent à la cause qui lui a donné naissance.
- Remarque : si la spire n'est pas complètement fermée, aucun courant ne peut circuler mais il apparaît une différence de potentiel entre les deux extrémités de la spire.
2. Champ électromoteur
a. Transformation non relativiste du champ électrique dans un changement de référentiel
- Utilisation de l'invariance de la force par changement de référentiel en mécanique classique.
- Utilisation de la loi de composition des vitesses.
- Loi de transformation du champ électrique : dans le référentiel relatif, un terme d'origine magnétique se rajoute.
b. Rappel : Loi d'Ohm pour un conducteur en régime continu et "basse fréquence"
- Loi d'Ohm locale
- Une différence de potentiel entre deux points d'un conducteur crée un champ électrique. Sous l'action de ce champ, les charges libres se déplacent donc créent un courant.
- On constate dans le cas des conducteurs dits "ohmiques" que le vecteur densité de courant est proportionnel au champ électrique. La constante de proportionnalité est la conductivité du conducteur.
- Domaine de validité : on admet que la loi d'ohm est valable en continu, et en sinusoïdal jusqu'à des fréquences de l'ordre de 1014 Hz.
- Interprétation microscopique de la loi d'ohm locale : modèle des collisions (modèle de Drude)
- Isotropie statistique de la vitesse des électrons de conduction après un choc,
- La moyenne mésoscopique (sur des petits éléments de volume) de la vitesse est proportionnelle à la moyenne mésoscopique du champ électrique, pour un temps moyen entre deux collisions. Le vecteur densité de courant est donc proportionnel au champ électrique.
- Sans revenir au modèle des collisions, il suffit de retenir que l'effet moyen des collisions sur la vitesse des électrons de conduction est analogue à celui d'un freinage visqueux.
- Passage à la loi d'Ohm macroscopique pour un conducteur filiforme : La différence de potentiel aux bornes d'un conducteur ohmique, en convention récepteur, est proportionnelle à l'intensité du courant qui le traverse. La constante de proportionnalité est la résistance électrique.
- Expression de la résistance d'un conducteur filiforme en fonction de sa conductivité, sa longueur et sa section.
c. Loi d'Ohm macroscopique généralisée en cas d'induction
- Dans un conducteur en l'absence de champ magnétique, l'existence d'un courant électrique ne provient que de la présence d'un champ électrique créé par une différence de potentiel électrique.
- Dans un conducteur fixe dans un champ magnétique variable ou/et mobile dans un champ magnétique stationnaire, l'existence d'un courant électrique provient également de la présence d'un champ électromoteur.
- La loi d'Ohm microscopique locale reste valable dans le référentiel lié au réseau métallique. En effet le modèle des collisions supposait les atomes du réseau métallique fixes.
- Passage à la loi d'Ohm généralisée macroscopique : il suffit de rajouter dans le schéma électrique du circuit une fém induite e orientée dans le sens du courant et de calculer cette fém e en effectuant la circulation du champ électromoteur dans le sens du courant également.
3. Induction électromagnétique dans un circuit fixe dans un champ magnétique variable (induction de Neumann)
a. Calcul de la f.e.m induite : Loi de Faraday
- Loi de Faraday à partir du champ électromoteur.
- Loi de Faraday à partir de l'équation de Maxwell Faraday.
- Retour à l'exemple expérimental.
b. Circuit filiforme fixe seul dans l'espace : phénomène d' autoinduction.
- Un circuit seul dans l'espace et parcouru par un courant i crée un champ magnétique dans tout l'espace. Le flux de ce champ à travers le circuit lui-même (flux propre) est proportionnel à i. Le coefficient de proportionnalité est l'inductance propre L (ou coefficient d' autolnduction) du circuit, exprimée en henry.
- L ne dépend que de la géométrie du système.
- L> 0 d'après la règle du tire - bouchon.
- Si l'intensité varie, le champ créé varie ainsi que le flux, d'où l'apparition d'une f .e.m induite dite d' autoinduction.
- Lien avec l' électrocinétique : schématisation par une bobine d'inductance L.
c. Bilan énergétique de l'établissement d'un courant dans un circuit filiforme indéformable et fixe.
- Etablir un courant i dans un circuit n'est pas gratuit d'un point de vue énergétique: il faut un apport égal à 1/2 L i2.
- On retrouve le fait que L> 0
- Cette énergie est stockée par le circuit et peut être récupérée : il s'agit donc d'une énergie potentielle.
- Etude du cas particulier du solénoïde long.
- Généralisation: l'énergie potentielle emmagasinée dans le circuit est en fait l'énergie magnétique emmagasinée dans le champ magnétique créé par ce circuit.
d. Deux circuits filiformes fixes dans l'espace : phénomène d'induction mutuelle.
- Soit un ensemble de deux circuits parcourus par des courants i1 et i2. Le flux du champ créé par le circuit 1 à travers le circuit 2 est proportionnel à i1. Le flux du champ crée par le circuit 2 à travers le circuit 1 est proportionnel à i2.
- On admet le théorème de Neumann : le coefficient de proportionnalité est le même dans les deux cas, et noté M (inductance mutuelle).
- M>0 ou M<0 .
- La variation d'un courant dans l'un des circuits induit une f.e.m d'induction mutuelle dans l'autre circuit. Les équations des circuits électriques sont donc couplées.
e. Bilan énergétique de l'établissement du courant dans un ensemble de deux circuits filiformes indéformables et fixes
- Etablir les courants i1 et i2 dans deux circuits n'est pas gratuit d'un point de vue énergétique : il faut un apport égal à 1/2 L1 i12 + 1/2 L2i22+ M i1i2
- Expression en fonction des flux.
- Cette énergie est stockée par les circuits et peut être récupérée : il s'agit donc d'une énergie potentielle.
- Cette énergie est l'énergie à fournir pour créer les champs magnétiques dans l'espace, elle est donc positive. On en déduit donc la relation M2<l < L1L2. Physiquement, cette inégalité traduit le fait qu'une partie des lignes de champ créées par un circuit ne traversent pas l'autre. A la limite, si les circuits sont très éloignés, aucune ligne de champ créée par un circuit ne traverse l'autre, on a M = 0.</l
- Dans le cas idéal d'un "couplage total", toutes les lignes de champ créées par un circuit traversent l'autre. On admet que l'on a alors M2<l = L1L2.</l
4. Induction électromagnétique dans un circuit mobile dans un champ magnétique stationnaire (induction de Lorentz)
- Circulation du champ électromoteur.
- On admet que la loi de Faraday est encore valable (on le vérifiera sur des exemples).
- Retour à l'exemple expérimental
Applications
1. Cas des circuits non filiformes
a. Les courants de Foucault
- Ce sont les courants induits dans les conducteurs non filiformes.
- La répartition de ces courants n'est pas simple: les courants de Foucault ont tendance à suivre le champ électromoteur (électrons libres mis en mouvement par ce champ), mais en bord de conducteur, le courant doit être tangentiel (condition limite évidente). Par contre la loi d'Ohm est toujours vérifiée (proportionnalité entre densité de courant et champ électrique dans le référentiel du conducteur).
- Cas où le conducteur est illimité, et les symétries et invariances sont simples :
- prévoir la forme des courants de Foucault en déterminant la forme des lignes de champ du champ électromoteur,
- détermination des courants de Foucault :
- Méthode 1 : calculer le champ électromoteur et en déduire le vecteur densité de courant de Foucault en écrivant la proportionnalité avec le champ électromoteur, le coefficient de proportionalité étant la conductivité. On admet en effet que le gradient du potentiel électrique est nul.
- Méthode 2 : calculer le champ électrique par circulation sur une ligne de champ électrique, et en déduire le vecteur densité de courant de Foucault en écrivant la proportionnalité avec le champ électrique, le coefficient de proportionalité étant la conductivité,
- Méthode 3 : déterminer les intensités élémentaires dans les boucles de courant de Foucault en écrivant la loi d'Ohm généralisée.
- Cas où le conducteur est limité :
- La méthodologie précédente reste valable si les conditions limites en bord de conducteur sont vérifiées.
- Sinon modéliser la forme des courants de façon simple en fonction du champ électromoteur et des symétries des bords du conducteur, et appliquer les méthodes 2 ou 3 précédentes.
- Effets de ces courants : ils sont prévisibles.
- Echauffement du conducteur, d'après la loi de Joule (principe du chauffage à induction).
- Freinage du conducteur s'il est en mouvement, d'après la loi de Lenz (principe du freinage électromagnétique des poids lourds).
b. Effet de peau dans un conducteur ohmique

- Description du phénomène :
- En régime indépendant du temps, les courants se répartissent uniformément dans la section des conducteurs. En régime alternatif haute fréquence, les courants ont tendance à se localiser au voisinage de la surface des conducteurs, sur une épaisseur typique appelée épaisseur de peau.
- Cette épaisseur de peau est d'autant plus faible que la fréquence du courant est élevée.
- Ce phénomène a pour conséquence d'augmenter la résistance du conducteur donc les pertes.
- Approche qualitative : La présence d'un courant dans le conducteur est à l'origine d'un champ magnétique, y compris dans le conducteur. Si ce courant est sinusoïdal, les courants de Foucault induits s'y opposent et annulent le courant au cœur du conducteur.
- Calcul à partir des équations de Maxwell :
- Equations de Maxwell dans un conducteur ohmique "en basse fréquence"
- Dans le domaine de validité de la loi d'ohm (f < 1014 Hz), on constate que le courant de déplacement est négligeable devant le courant de conduction. L'étude du conducteur se fait donc dans l'ARQS bien que la fréquence puisse être supérieure à la limite usuelle de l'étude des circuits dans l'ARQS (106 Hz).
- Les excédents locaux de charges tendent très rapidement vers 0 dans le cas des conducteurs, on peut donc considérer que la densité volumique de charge est toujours nulle dans un conducteur (le conducteur peut par contre être chargé en surface). La démonstration mathématique repose sur l'équation de Maxwell-Gauss (création d'un champ par un excédent de charge), la loi d'ohm locale (écoulement des charges sous l'action de ce champ) et l'équation de conservation de la charge (diminution de l'excédent de charge grâce à l'écoulement de charge).
- Equation vérifiée par la densité de courant (ou le champ électrique car proportionnalité entre les deux) : c'est une équation de diffusion (voir cours sur la diffusion).
- Résolution de l'équation de diffusion dans le cas d'un demi-espace conducteur limité par un plan. Ce modèle est valable lorsque l'épaisseur de peau est très faible devant le rayon du conducteur.
- Equations de Maxwell dans un conducteur ohmique "en basse fréquence"
- Limite du conducteur parfait.
- Un conducteur parfait est un modèle de conducteur de conductivité infinie.
- L'épaisseur de peau tend vers 0, la conduction du courant est donc surfacique.
- Argument énergétique pour interpréter la conduction surfacique.
2. Couplage électromécanique
a. Mise en évidence sur les rails de Laplace
- Description du dispositif.
- Analyse physique.
- Vérification de la loi de Faraday.
- Conversion de puissance :
- équation électrique
- équation mécanique
- conversion électromécanique : on constate que Plaplace + ei = 0 : il y a couplage électromécanique parfait. On admet la généralité de ce résultat pour tout circuit mobile dans un champ magnétique stationnaire.
- Bilan énergétique
b. Exemple du haut-parleur électrodynamique
- Description du haut-parleur.
- Analyse physique.
- Equation mécanique.
- Equation électrique.
- Les deux équations différentielles précédentes sont couplées, elles peuvent se découpler. L'usage de la notation complexe simplifie les calculs.
- Détermination de l'impédance équivalente du haut-parleur : elle est constituée d'une impédance dite "électrique" et d'une impédance dite "motionnelle" (qui contient les caractéristiques mécanique du haut-parleur).
- Bilan énergétique :
- Technique : multiplication du PFD par la vitesse, multiplication de la loi de maille par l'intensité électrique.
- Conversion de puissance : on a bien Plaplace + ei = 0.
- Bilan énergétique global
3. Autres applications de l'induction
- Avec couplage électromécanique :
- Les moteurs électriques : ils convertissent une énergie électrique en énergie mécanique.
- Les générateurs électriques : ils convertissent une énergie mécanique en énergie électrique.
- Sans couplage électromécanique :
- Les antennes : courant induit ou f.e.m induite par les variations du champ magnétique d'une onde électromagnétique.
- Le transformateur : transforme une tension alternative en une autre tension alternative (circuits couplés).























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !