Chapitres
- 01. Définition
- 02. Un peu d'histoire
- 03. Calculs
- 04. Les lois de Kepler
- 05. Accélération

Définition
La vitesse est une grandeur physique qui est définie par une évolution face au temps. La vitesse ne définit pas qu'uniquement la vitesse de déplacement mais peut aussi correspondre à la vitesse de réaction chimique ou encore une vitesse de séchage par exemple. En règle générale, une vitesse est égale à la division de la mesure d'une variation telle qu'une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation. L'exemple le plus simple est celui de la vitesse de déplacement. Il s'agit d'une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.
Un peu d'histoire

Il a fallu attendre Galilée pour qu'une définition de la vitesse soit donnée. En effet, les mathématiciens refusaient de faire le quotient de deux grandeurs si celles-ci n'étaient pas homogènes. De ce fait, diviser une distance par un temps leur semblait absolument invraisemblable au même titre que l'addition de ces deux grandeurs.
Galilée décida de comparer le rapport des distances parcourues par des corps définis avec le rapport de temps qui leur correspondait. Il obtint donc l'équivalence suivante :  Pour Aristote, tout corps qui tombe possède une vitesse qui sera déterminée par la nature et celle-ci ne peut pas évoluer, cela signifie que pour lui cette vitesse ne peut ni augmenter ni diminuer sauf en usant de la violence ou en mettant en place une résistance.
Pour Aristote, tout corps qui tombe possède une vitesse qui sera déterminée par la nature et celle-ci ne peut pas évoluer, cela signifie que pour lui cette vitesse ne peut ni augmenter ni diminuer sauf en usant de la violence ou en mettant en place une résistance.
De ce fait, pour Aristote, un objet mobile dix fois plus lourd qu'un autre se déplacera dix fois plus vite et tombera également dix fois plus vite. Mais cette idée sera démontée par Galilée dans le De motu lorsqu'il énoncera la loi de la chute des corps. Cette loi détermine que les corps chutent selon un mouvement uniformément accéléré et que peu importe la taille, les dimensions ou les natures (sauf dans le cas d'une chute dans le vide) tombent avec la même vitesse. Il ajoutera, puisqu'il ne connait pas la pesanteur terrestre, que l'accélération de la chute correspond à une constante universelle.
Tout cela mis alors fin à l'Aristotélicisme. Il faudra tout de même attendre le 5 Juillet 1698 pour que la notion de vitesse instantanée soit définie de façon formelle par Pierre Varignon. En effet, celui-ci décrira la vitesse instantanée comme étant le rapport d'une longueur infiniment petite dx sur un temps infiniment petit dt mis afin de parcourir cette longueur. Pour cela, il utilisera le formalisme du calcul différentiel qui a été défini par Gottfried Wilhelm Leibniz il y a 14 ans de cela.
Calculs
En règle générale, une vitesse se calcule avec la formule suivante :
vitesse moyenne du parcours = distance parcourue / temps de parcours.
Dans le système international (SI), la vitesse cinématique est le mètre par seconde et se note m/s ou m.s-1. Dans le système usuel, on préférera le kilomètre par heure qui se note km/h ou km.h-1. Dans la marine, on préférera le nœud, qui représente 0,5144 m/s. On trouvera même dans certains cas, dans l'aviation par exemple, le nombre de Mach. Mach 1 est égale à la vitesse du son. Attention, cette vitesse dépend de la température.
Le vecteur vitesse

On appelle vecteur vitesse instantanée le vecteur défini par la dérivée suivante :  Avec :
Avec :
- r (t) le vecteur définissant la position de l'objet à un instant t.
La vitesse de réaction au sein d'un mélange chimique
Définition
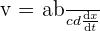 avec :
avec :
- v : vitesse volumique de réaction (en mol.m-3.s-1) ;
- V : volume de la solution (en m3) ;
- dx : variation de l'avancement (en mol) ;
- dt : durée de la variation (en s).
Remarques
- Il arrive fréquemment que le volume V soit exprimé en litre. La vitesse de réaction est alors exprimée en mol.L-1.s-1 ;
- Si la transformation est lente ou très lente la durée peut être exprimée en minute ou en heure. La vitesse de réaction est alors exprimée en mol.L-1.min-1 ou en mol.L-1.h-1 ;
- Le rapport dx/dt représente la dérivée par rapport au temps de l'avancement.
Ce qu'il faut connaître pour déterminer v
D'après la relation de définition , il faut connaître V et la fonction x=f(t). Cette fonction peut être connue soit:
- Par son graphe (il est donné dans certains exercices) ;
- Par un tableau de mesures présentant les valeurs des couples {ti ; xi} (il est donné dans certains exercices) ;
- A l'aide du tableau d'avancement de la réaction. Il faut alors connaître,soit par une méthode chimique soit par une méthode physique, l'évolution de la concentration de l'un des réactifs ou de l'un des produits de la transformation. Etudier les deux TP de cinétique chimique.
Méthodes
- Graphiquement: On trace la tangente à la courbe x=f(t) à la date t choisie. La valeur du rapport dx/dt est égal au coefficient directeur de cette tangente ;
- On divise alors cette valeur par la valeur de V (volume de la solution) ;
- Par le calcul: Un tableur calcule directement la vitesse v à partir des valeurs de V, ti et xi.
Evolution de la vitesse de réaction au cours du temps
Au cours du temps les réactifs disparaissent donc leur concentration diminue. Or nous avons déjà vu que la concentration des réactifs est un facteur cinétique. Plus la concentration des réactifs est faible plus la réaction est lente. Donc, en général, au cours du temps la vitesse de réaction diminue.
Le Système International, rappel
L'ensemble des unités associées aux dimensions fondamentales constitue le système international d'unités. Il s'agit du système MksA (mètre, kilogramme, seconde, Ampère), mais le Kelvin, le mole et le candela font aussi partie de ce système. Ces unités sont appelées unités légales. Elles sont universelles et connues de par le monde entier.
Il est important de savoir que toutes les autres dimensions se déduisent de ces sept dimensions fondamentales par produit ou division de ces dimensions.
Dans certains sujets d'exercices, les grandeurs ne sont pas exprimées dans le système international mais avec des grandeurs usuelles. Il est facile de les comprendre et elles sont parfois utilisées dans la vie de tous les jours, mais il est essentiel de toujours effectuer les calculs avec les grandeurs exprimées dans l'unité internationale pour éviter les erreurs. Par exemple, la pression est souvent exprimée en Bar. Or, dans le système international, la pression s'exprime en Pascal !
Les lois de Kepler
Les lois de Kepler sont des lois relatives à la vitesse ainsi qu'à l'accélération. Voici l'énoncé de de la seconde loi de Kepler :
Quand une planète parcourt son orbite, le rayon Soleil-planète balaie des aires égaux en des intervalles de temps égaux
Cette loi s'applique à la vitesse de déplacement d'une planète autour de son orbite. Comme les orbites sont elliptiques, afin de parcourir une aire donnée, il faut que la planète parcourt une distance plus grande quand elle est proche du soleil et une distance plus petite quand elle est loin du soleil. La seconde loi de Kepler sert donc à lier la vitesse et la distance des planètes selon leur proximité avec le soleil.

Accélération
L'accélération est le phénomène attenant à l'augmentation de la vitesse. L'accélération est égale à la dérivée de la vitesse instantanée. C'est à dire que la fonction dérivée de la fonction qui détermine la position d'un point selon le temps est l'accélération. Il s'agit d'une grandeur physique qui s'exprime sous la forme de vecteur. Comme la vitesse, il s'agit d'une variation au cours du temps. La norme de ce vecteur est l'accélération. Selon le système international, l'accélération a pour unité le mètre par seconde carré qui se note m.s-2.
Les débuts de cette notion
C'est en 1700 qu'un père jésuite français, Pierre Varignon, commence à identifier l'existence de l'accélération dans ces calculs. En effet, ce mathématicien a été l'un des premiers à chercher à comprendre le principe de la vitesse.
Approche graphique
Lors d'un courbe d'accélération, quand la vitesse est maximale, l'accélération est minimale.
Calculs
On peut effectuer différents calculs sur l'accélération. Voici ceux que vous pourriez être amenés à effectuer.
Accélération moyenne

Accélération instantanée

Rappels sur la dérivation
Dérivation d'une fonction usuelle
Pour tout réel y et et pour tout entier naturel n, les fonctions suivantes se dérivent selon les formules ci-dessous. y une fois dérivé devient 0. Cette fonction linéaire est définie sur ℝ est son domaine de dérivabilité sera lui aussi ℝ. x dérivé devient 1, toujours défini et dérivable sur ℝ. Dans le cas d'une fonction puissance comme xn où n est supérieur ou égal à 1, la dérivée de la fonction sera nxn-1. Ces deux fonctions sont toujours définies et dérivables sur ℝ. Pour les fonctions racines, elles sont définies sur ℝ* et dérivables sur ℝ*. Pour une fonction de ce type, 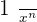 la fonction dérivée sera
la fonction dérivée sera 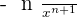 Pour la fonction racine carré, définie sur ℝ+, elle sera dérivable sur ℝ*. La fonctionne racine carré de x se dérive en :
Pour la fonction racine carré, définie sur ℝ+, elle sera dérivable sur ℝ*. La fonctionne racine carré de x se dérive en : 
Dériver sur un intervalle donné
On considère qu'une fonction f est dérivable sur un intervalle I à condition et uniquement si elle est dérivable sur tout réel de cet intervalle. La fonction dérivée de f est alors f'. Cette dernière associe à tout réel x une image f' (x). Si la fonction f est dérivable sur un intervalle I et si f' est également dérivable sur le même intervalle I, alors la dérivée de f', notée f'' et appelée dérivée seconde de f ou dérivée d'ordre 2 de f existe.























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Si on donne : V=At3-Bt oú t représente le temps alors quels seraient les unités SI de A et B?
Bonjour, nous serions ravis de vous aider ! Avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique « Découvrir nos Superprofs » en indiquant les mathématiques. Vous trouverez de nombreux professeurs près de chez vous. Excellente journée ! :)
Je voudrais soutirer de l’explication á propos d’un exercise s’il vous plaît
Bonjour, nous serions ravis de vous aider ! Avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique « Découvrir nos Superprofs » en indiquant la matière des mathématiques. Vous trouverez de nombreux professeurs près de chez vous. Excellente journée ! :)
Site Génial, vraiment merci!!! Info non-truqué et hyper utile!! Merci à vous de m’avoir fait découvert le site!!!
Merci infiniment pour cette utile et précieuse information. Super votre blog, bravo !