Chapitres
- 01. Rappels sur la Loi de Laplace
- 02. Révisions : notions à maîtriser
- 03. Exercice d'application : les bulles de savon
- 04. Exercice d'application : La différence entre pression et volume
- 05. Exercice d'application : Le rail de Laplace
- 06. Exercice d'application : Le coefficient de Laplace en musique

Rappels sur la Loi de Laplace
En mécanique des fluides
En physique, la loi de Laplace, également appelée équation de Laplace-Young, représente une loi qui lie la courbure locale de l'interface séparant deux milieux à la différence de pression entre les deux milieux. On peut alors appeler cette pression : pression de Laplace.
Ainsi, pour un système qui comporte deux milieux non miscibles séparés par une interface, on dit qu'il y a une différence de pression entre les deux milieux lorsque cette interface présente une courbure. En effet, la pression est plus grande dans une goutte de pluie ou alors dans une bulle de savon que dans l'atmosphère qui peut les entourer. Ce qui provoque cette différence de pression est la tension de surface mais aussi la courbure de moyenne surface.
Thomas Young, en 1804, présenta devant la Royal Society of London une description de la capilarité. D'ailleurs, cette présentation sera publiée dans les Philosophical Transactions l'année qui suivra. Dans cette présentation, Young y décrira de façon très précise la force qui va attirer les fluides vers le centre de courbure d'une surface et relie cette force à la somme des courbures selon les deux direction orthogonales, introduisant ainsi la notion de courbure moyenne d'une surface.
La Royal Society of London for the Improvement of Natural Knowledge, abrégée en Royal Society, est l’institution des sciences en Angleterre. Fondée en 1660 à Londres, elle est au Royaume-Uni l’équivalent de l’Académie des sciences en France.
Pour cela, Young se basa sur les lois de l'hydrostatique pour relier les mesures d'ascension capillaire avec l'angle de contact entre le fluide et la paroi du tube capillaire. On lui reprocha cependant l'absence d'analyse mathématique de la courbure.
Laplace reprendra un an plus tard les observation de Young qui publiera la Théorie de l'action capillaire en supplément du tome dix de son ouvrage Mécanique céleste. Il présentera dans ce supplément l'analyse mathématique de la courbure moyenne d'une surface qui manquait à l'étude de Young. Ainsi, il rendra compte des résultats de ce dernier, expliquant ainsi pour on nomme cette équation : équation de Laplace-Young.

En thermodynamique
La thermochimie correspond à une branche de la physique chimie et permet l'étude des différents phénomènes thermiques dans des milieux réactionnels. On peut positionner cette branche, sur le plan disciplinaire, à l'interface entre la chimie et la thermodynamique.
En chimie, il existe différents types de réactions : les réactions dites exothermiques et qui dégagent donc de la chaleur et les réactions dites endothermiques qui, quant à elles, absorbent la chaleur. Il est possible de déterminer et mesurer les chaleurs de réactions par calorimétrie à pression constante dans un calorimètre ou encore à volume constant dans une bombe calorimétrique.
La bombe calorimétrique, inventée en 1881 par Marcellin Berthelot, est un outil permettant de mesurer le pouvoir calorifique d'une combustible. C'est pour cela que Marcellin Berthelot est considéré comme étant le fondateur de la thermochimie. Même s'il faudra attendre le XXe siècle que la thermochimie se développera considérablement.
En appliquant le deuxième principe de la thermodynamique aux systèmes chimiques, il est possible de prévoir le sens des réactions mais aussi le positionnement des équilibres chimiques et ainsi de définir le rendement et la composition d'un système après la réaction.
Les lois de la thermodynamique
Il est important de noter que le premier et le deuxième principe de la thermodynamique sont les plus importants, mais il peut tout de même intéressant de connaître les deux autres.
Le principe zéro de la thermodynamique
Ce principe concerne la notion d'équilibre thermique. Ainsi, il est à la base de la thermométrie et s'énonce ainsi : si deux systèmes sont en équilibre thermique avec un troisième, alors ils sont aussi ensemble en équilibre thermique.
Le premier principe de la thermodynamique
Egalement appelé principe de la conservation de l'énergie, ce principe affirme que l'énergie est toujours conservée. Formulé autrement, cela signifie que l'énergie totale d'un système isolé reste constante. Ainsi, les événements qui se produisent au sein du système isolé ne se traduisent donc que par des transformations de certaines formes d'énergie en d'autres formes d'énergie. Puisque l'énergie ne peut pas être produite en partant de rien, elle est présente en quantité invariable dans la nature. Elle ne peut donc que se transmettre d'un système à un autre : on ne crée par l'énergie, on la transforme.
Ce principe est également considéré comme étant une loi générale pour toutes les théories physiques, notamment en mécanique, électromagnétisme ou physique nucléaire puisqu'on ne lui a jamais trouvé la moindre exception même si des doutes peuvent subsister lorsque l'on étudie les désintégration radioactives.
De puis le théorème de Noether, on sait que la conservation de l'énergie est intimement reliée à une uniformité de structure de l'espace-temps.
Le premier principe de la thermodynamique rejoint alors le célèbre principe popularisé par Lavoisier : "Rien ne se perd, rien ne se crée, tout se transforme."
Le deuxième principe de la thermodynamique
Egalement appelé principe d'évolution des système, ce principe affirme la dégradation de l'énergie. En effet, l'énergie d'un système passe de façon nécessaire et spontanée de formes concentrées et potentielles à des formes diffuses et cinétiques telles que le frottement ou la chaleur.
Ce principe introduit donc également la notion d'irréversibilité d'une transformation et la notion d'entropie. En effet, d'après le deuxième principe de la thermodynamique, l'entropie d'un système isolé augmente ou reste constante. Souvent interprété comme une mesure du désordre et comme l'impossibilité du passage du désordre à l'ordre sans intervention extérieur.
L'interprétation de ce principe se base sur la théorie de l'information de Claude Shannon et la mesure de cette information, également appelée entropie de Shannon.
La principale différence de ce principe avec le premier principe de la thermodynamique est l'origine statique de ce deuxième principe. En effet, les lois microscopiques qui gouvernent la matière ne le contiennent qu'implicitement et de manière statique. Cependant, le deuxième principe de la thermodynamique reste relativement indépendant des caractéristique des lois précédemment citée puisqu'il apparaît même si l'on suppose des lois simplistes à petite échelle.
Le troisième principe de la thermodynamique
Ce principe, quant à lui, est associé à la descente vers un état quantique fondamental d'un système dont la température s'approche d'une limite qui définit la notion de zéro absolu. En effet, en thermodynamique classique, ce principe permet de calculer l'entropie molaire S d'un corps pur par intégration sur la température à partir de S=0 à 0 K dans le but d'établir des tables de données thermodynamiques.
Principes importants de cette branche
Chaleur de réaction

Au cours d'une réaction chimique, on dit que le système échange de l'énergie avec le milieu extérieur. Cet échange se fait sous la forme de transfert thermique, anciennement appelé chaleur.
Cette énergie échangée sous forme de transfert thermique Q dépend des conditions expérimentales dans lesquelles se produit la réaction :
- Volume constant, on parle d'une transformation isochore, la thermodynamique montre que Q est égale à la variation d'énergie interne du système. On peut alors noter Qv = ΔU (c'est notamment le cas de la bombe calorimétrique)
- Pression constante, la chaleur est égale à la variation d’enthalpie : Qp = ΔH (ce qui représente le cas très fréquent des réactions effectuées à l’air libre).
Enthalpie libre
Pour tout système thermodynamique, il est défini une fonction d'état appelée enthalpie libre ou encore énergie de Gibbs. Cette fonction, notée G, est telle que G = H - TS avec :
- H l'enthalpie en joules
- T la température en kelvin
- et S l'entropie en J.K-1
Cette fonction d'enthalpie libre est une fonction d'état considérée comme indispensable pour l'étude des équilibres chimiques. En effet, cette fonction ne peut que décroître dans le cas d'une transformation à pression et température constantes selon le deuxième principe de la thermodynamique. Cela permet donc, dans le cas d'une réaction chimique effectuée à T et P constantes, d'avoir le signe de l'enthalpie libre de réaction qui indique le sens dans lequel se déplace l'équilibre chimique. Ainsi, lorsque l'enthalpie libre atteint un minimum et donc qu'elle ne varie plus, alors l'équilibre chimique est atteint.
Révisions : notions à maîtriser
- Descriptions microscopique et macroscopique d’un système à l'équilibre
- Échelles microscopique, mésoscopique, et macroscopique. Libre parcours moyen.
- Description des caractères généraux de la distribution des vitesses moléculaires d'un gaz (homogénéité et isotropie).
- Vitesse quadratique moyenne.
- Pression cinétique.
- Température cinétique.
- Exemple du gaz parfait monoatomique : Ec=3/2kT.
- Système thermodynamique.
- État d’équilibre d’un système soumis aux seules forces de pression.
- Pression, température, volume, équation d’état.
- Grandeur extensive, grandeur intensive.
- Exemples du gaz parfait et d’une phase condensée indilatable et incompressible.
- Énergie interne d’un système. Capacité thermique à volume constant dans le cas du gaz parfait.
- Énergie interne et capacité thermique à volume constant d’une phase condensée considérée incompressible et indilatable.
- Approximation des phases condensées peu compressibles et peu dilatables.
- Du gaz réel au gaz parfait.
- Corps pur diphasé en équilibre.
- Diagramme de phases (P,T).
- Cas de l’équilibre liquide-vapeur : diagramme de Clapeyron (P,v), titre en vapeur.
- Équilibre liquide-vapeur de l’eau en présence d’une atmosphère inerte.
Exercice d'application : les bulles de savon

Une bulle de savon sphérique, de rayon r, contient n moles d’air, assimilé à un gaz parfait, à la pression Pi et à la température T0. L’air extérieur est à la température T0 et à la pression P0.
On admet que le travail élémentaire à fournir pour augmenter réversiblement de dΣ la surface Σ de la bulle est δW = 2γ(T).dΣ où γ(T) est le coefficient de tension superficielle.
On étudie l’augmentation de la surface de la bulle de savon à température et pression extérieures constantes.
1 - Montrer que le potentiel thermodynamique de la transformation est G*.
2 - Le rayon de la bulle passe réversible ment de r à r + dr. Exprimer dG* en fonction de dr.
3 - En déduire la différence de pression Pi - P0 entre l’intérieur et l’extérieur de la bulle en fonction de γ(T0) et du rayon de la bulle à l’équilibre, req.
Exercice d'application : La différence entre pression et volume
1 - Exprimer la relation entre la pression et le volume à chaque instant d'une transformation quasi-statique adiabatique d'un gaz parfait en contact permanent avec les parois de son récipient.
2 - Retrouver cette relation à partir des identités thermodynamiques.
Solution
- Système : Le gaz parfait seul.
- dU = δW à chaque instant pour une transformation adiabatique
- δW = - pdV travail reçu par le gaz à chaque instant de la part des parois du récipient
- dU = nCvm dT et pV = nRT pour un gaz parfait
- d'où nCvm dT/T = - nRdV/V qui donne la relation différentielle avec les variables V et T
- dp/p + dV/V = dT/T en utilisant la différentielle logarithmique de pV = nRT
- d'où nCvm dp/p + (nCvm + nR) dV/V = 0
- soit Cvm dp/p + Cpm dV/V = 0
- ou bien dp/p + γ dV/V = 0 avec γ = Cpm / Cvm
- d'où, par intégration pVγ = Cte (loi de Laplace)
- Au cours de la transformation, il n'y a aucune cause d'irréversibilité : Gaz parfait et absence de discontinuité non infinitésimale de température ou de pression.
- La transformation est donc isentropique, dS = 0.
- dU = TdS - pdV identité thermodynamique pour un fluide
- dU = nCvm dT et pV = nRT pour un gaz parfait
- d'où dS = nCvm dT/T + nRdV/V
- Or dS = 0
- donc nCvm dT/T = - nRdV/V
- Le reste de la démonstration est identique à la précédente.
Exercice d'application : Le rail de Laplace
Une tige métallique de masse m glisse sans frottements sur deux rails métalliques inclinés d’un angle α par rapport à l’horizontale, distants de d. Les rails, la tige et la bobine d’inductance L constituent un circuit électrique. Ce circuit est plongé dans un champ magnétique B vertical et uniforme.
A t = 0, on lâche la barre.
1- Déterminer son mouvement ultérieur sachant qu’elle reste toujours horizontale.
2 - Faire un bilan énergétique.
Exercice d'application : Le coefficient de Laplace en musique
Les orgues les plus imposantes peuvent comporter de 2000 à 4000 tuyaux sonores. Certains tuyaux, comme ceux appartenant au jeu de "montre", sont ouverts à leurs deux extrémités. L'air est insufflé par une soufflerie au niveau de leur base.
Un tuyau d'orgue de longueur L émet un son de hauteur déterminée qui dépend de la température ambiante.
Un musicien affirme que :
"Une augmentation de température de 10 °C modifie la hauteur de la note d'un quart de ton !"
Dans ce problème, on souhaite valider cette affirmation. On étudie pour cela la note jouée par un tuyau métallique à embouchure de flûte appartenant à un jeu de "montre".

Données :
- Modèle théorique du tuyau ouvert/ouvert (ouvert aux deux extrémités).
- Lorsqu'une colonne d'air est excitée, un son est alors émis ;
- La longueur d'onde du son émis est égale au double de la longueur du tuyau : λ = 2 . L
- Conversion Kelvin - degré Celsius
- T(K) = q(°C) + 273
- Longueur du tuyau d'orgue étudié à 20 °C
- L = 52,0 cm
Questions préliminaires
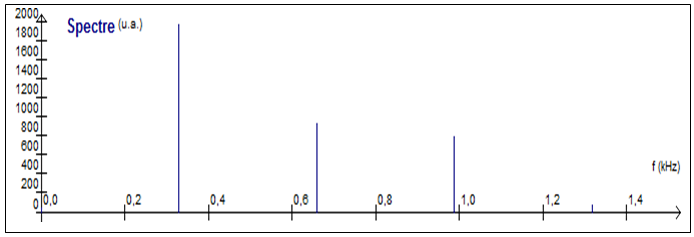
1. Déterminer la note jouée par le tuyau étudié. Le candidat cherchera à obtenir la meilleure précision possible et s'assurera que les deux graphiques (documents 1 et 2) sont cohérents.
2. Discuter qualitativement l'influence d'une variation de température sur la hauteur du son produit.
Problème
3. Déterminer quantitativement si l'affirmation du musicien sur l'évolution de la hauteur du son est correcte. Un calcul numérique est attendu.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n'a pas abouti. La démarche suivie est évaluée et nécessite d'être correctement présentée.

Document 3 – Construction de la gamme tempérée :
La gamme musicale qui est utilisée de nos jours, a été élaborée à la fin du XVIIème siècle. Elle est fondée sur une série de notes (Do - Do# - Ré - Mib - Mi - Fa - Fa# - Sol - Sol# - La - La# - Si - Do) qui se répètent. Chaque série constitue une octave et chaque octave est numérotée
(cf. Document 4). Ainsi le La3 correspond à la note La de la 3ème octave.
Chaque octave est découpée en douze intervalles égaux, appelés demi-tons (noté ½ ton).

À chaque note est associée une fréquence f exprimée en hertz. Par convention, la fréquence de la note La3 a été fixée à 440 Hz.
La gamme tempérée est construite pour que le rapport entre la fréquence d’une note et la fréquence de la même note de l’octave du dessous vaut 2.
La division en 12 intervalles égaux de l’octave implique que le rapport de fréquences du demi-ton est égal à : \[ \sqrt [12] {2} = (2) ^ { \frac {1} {12} } = 1.059\]
Ainsi, la fréquence de la note La#3 s’obtient en calculant : f(La#3) = 1,059 × f(La3) = 466 Hz
Document 4 – Tableau de correspondance entre note de musique et fréquence (en Hz) :
| Note \ Octave | Do | Do# | Ré | Mib | Mi | Fa | Fa# | Sol | Sol# | La | La# | Si |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 130 | 139 | 147 | 156 | 165 | 175 | 185 | 196 | 208 | 220 | 233 | 247 |
| 3 | 262 | 277 | 294 | 311 | 330 | 349 | 370 | 392 | 415 | 440 | 466 | 494 |
| 4 | 523 | 554 | 587 | 622 | 659 | 698 | 740 | 784 | 831 | 880 | 932 | 988 |
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !