Chapitres
- 01. Exercice n° 1
- 02. Exercice n° 2
- 03. Exercice n° 3
- 04. Exercice n° 4
- 05. Exercice n° 5
- 06. • Exercice n° 6
- 07. Exercice n° 7
- 08. Exercice n° 8
- 09. Exercice 9
- 10. Exercice 10

Exercice n° 1
La masse d'un corps se mesure avec une balance et s'exprime en kilogramme (kg).
Le poids d'un corps se mesure à l'aide d'un dynamomètre et s'exprime en Newton (N).
Exercice n° 2
Quelles sont les caractéristiques du poids d'un corps ? Les caractéristiques du poids d'un corps sont la direction, le sens et la direction.
De quoi dépend le poids d'un corps sur Terre ? Le poids d'un corps sur Terre dépend de l'altitude et de la latitude (du lieu).
Quelle est la relation entre poids et masse sur Terre (préciser les unités) ? La relation entre poids et masse sur Terre est P = M × g P --> N M --> kg g --> N/kg

Exercice n° 3
Où se trouve le centre de gravité d'un disque, d'une surface rectangulaire, d'une sphère, d'un anneau circulaire ? Le centre de gravité d'un disque est le centre de celui-ci. Le centre de gravité d'une surface rectangulaire est l'intersection de ces diagonales. Le centre de gravité d'une sphère est le centre de celui-ci. Le centre de gravité d'un anneau circulaire est le centre du disque limité par l'anneau.
Exercice n° 4
Quel est sur Terre le poids d'un corps dont la masse est 50 kg ? M = 50 kg g = 9,8 N/kg P = ? P = M × g P = 50 × 9,8 P = 490 N
Quel est le poids d'une pomme de masse 102 g ? M = 102 g = 0,102 kg g = 9,8 N/kg P = ? P = M × g P = 0,102 × 9,8 P = 0,99 N
Quel est le poids d'une grue de masse 2 tonnes ? M = 2 t = 2 000 kg g = 9,8 N/kg P = ? P = M × g P = 2 000 × 9,8 P = 19 600 N
Exercice n° 5
Quelle est la masse d'un corps dont le poids sur Terre est 49 N ? P = 49 N g = 9,8 N/kg M= ? P = M × g M = P/g M = 49/9,8 M = 5 kg • Le décanewton (daN) est une unité de poids utilisée (1 daN = 10 N).
Quelle est la masse d'un corps dont le poids est 1 000 daN ? P = 1 000 daN = 10 000 N g = 9,8 N/kg M= ? P = M × g M = P/g M = 49/9,8 M = 1 020 kg
Où trouver un bon cours de physique ?
• Exercice n° 6
• Calculez votre poids en Newton, puis en décanewton. M = .. kg g = 9,8 N/kg P = ? P = M × g P = .. × 9,8 P = .. N
Un pèse personne est souvent une balance à ressort :
Mesure-t-il une masse ou un poids ? Il mesure un poids en réalité.
Il est gradué en kg. Quelle est en réalité l'unité ? L'unité réelle est le daN.
Comment progresser en cours physique chimie college ?
Exercice n° 7
Un objet a une masse de 30 kg sur Terre :
Quel est son poids sur la Lune ? M = 30 kg g = 1,62 N/kg P = ? P = M × g P = 30 × 1,62 P = 48 N
Quel serait son poids sur Mars ? M = 30 kg g = 3,6 N/kg P = ? P = M × g P = 30 × 3,6 P = 108 N
Exercice n° 8
Le 21 juillet 1969, les premiers hommes ont débarqué sur la Lune (Mission Apollo 11 dont l'équipage était composée de Armstrong, Collins et Aldrin). Ils ont rapporté sur Terre 22 kg d'échantillons lunaire.

Quel était le poids de ces échantillons sur la Lune ? Quel était leur poids sur Terre ?
Poids sur la Lune :
M = 22 kg PL = ?
P = M × g P = 22 × 1,6 P = 35,2 N
Poids sur la Terre :
M = 22 kg g = 9,8 N/kg PT = ?
P = M × g P = 22 × 9,8 P = 215,6 N
Quel était le poids de Armstrong à la surface de la Lune sachant que sur la Terre, il valait 745 N ?
PT = 745 N g = 9,8 N/kg M = ?
P = M × g M = P/g M = 745/9,8 M = 76 kg
M = 76 kg g = 1,6 N/kg PL = ?
P = M × g P = 76 × 1,6 P = 121,6 N
Retrouvez tous nos cours de physique chimie seconde.
Exercice 9
On se propose dans cet exercice de faire une plongée au cœur de l'effervescence d'une boisson gazeuse, d'illustrer et d'interpréter sous l'angle de la physico-chimie les différentes étapes de la vie éphémère d'une bulle, à savoir : sa naissance, son ascension dans le liquide, et son éclatement en surface.
Dans tout l'exercice les bulles seront assimilées à des sphères, et la boisson à un liquide de masse volumique égale à celle de l'eau. Le référentiel d'étude est terrestre considéré comme galiléen.
Données :
Masses volumiques : eau re = 1,0´103 kg.m-3; dioxyde de carbone rdc = 1,8 kg.m-3
Intensité de la pesanteur: g = 10 m.s-2.
1. Naissance et décollement d'une bulle
Dans une bouteille fermée de boisson gazeuse, un équilibre s'établit entre le dioxyde de carbone qui est dissous dans la boisson et le dioxyde de carbone gazeux piégé dans le col de la bouteille. Lors de l'ouverture de celle-ci, l'équilibre est rompu et la boisson se débarrasse d'une partie du dioxyde de carbone dissous qui retourne progressivement en phase gazeuse. Il y a formation de bulles qui vont s'enrichir continûment en gaz au cours de leur remontée.
Dans un verre, les bulles naissent sur des sites de nucléation qui sont des embryons de bulles présents en solution ou de petites poches d'air piégées par des impuretés microscopiques (fibres de cellulose, microcristaux …). La figure 1 illustre cette formation de bulles sur un site de nucléation.
Dès que la valeur de la poussée d'Archimède à laquelle la bulle est soumise dépasse la valeur de la force capillaire qui l'ancre à son site de nucléation, la bulle se détache. Puis une autre bulle naît et subit le même sort.

Pour une bulle qui vient de se détacher du site de nucléation dans un liquide de masse volumique re :
Donner la direction et le sens de la poussée d'Archimède qui s'exerce sur une bulle de volume V0 dans la boisson.
Donner l'expression littérale de sa valeur en fonction du volume V0 de la bulle.
1.1 Ascension d'une bulle : à la recherche d'une modélisation satisfaisante
À l'instant de date t0 = 0 s, une bulle de rayon r0 = 20 mm, située au
point A à la profondeur z0 = 0 m dans le repère (O ; ) (figure 2) se détache de son site de nucléation avec une vitesse initiale v0 nulle
dans le référentiel terrestre supposé galiléen. Elle remonte verticalement vers la surface S du liquide, qu'elle atteint avec une vitesse vS d'environ 15 cm.s-1.
Dans un premier temps (pour les questions 2.1. et 2.2.), on assimile la bulle de gaz à une sphère dont le volume ne varie pas lors de sa remontée.
2.1. Étude du mouvement d'une bulle en l'absence de force de frottement
Montrer que le poids de la bulle a une valeur négligeable devant celle de la poussée d'Archimède en calculant le rapport: .
En utilisant la deuxième loi de Newton, établir l'expression de la coordonnée az du vecteur accélération de la bulle en fonction des masses volumiques re et rdc et de g.
En déduire l'expression de la valeur de la vitesse de la bulle en fonction du temps.
Montrer que la durée ts théoriquement nécessaire pour que la bulle atteigne la surface avec la vitesse vs est alors d'environ trente microsecondes.
Cette valeur correspond-elle aux observations de la vie quotidienne ? Conclure quant à la validité du odèle proposé.
2.2. Étude du mouvement de la bulle en présence d'une force de frottement
Le liquide exerce sur la bulle une force de frottement, proportionnelle à sa vitesse, qui peut s'écrire vectoriellement , k est un coefficient qui dépend du rayon de la bulle et de la viscosité du fluide dans lequel elle se déplace.
Représenter schématiquement, sans souci d'échelle, les forces non négligeables qui s'exercent sur la bulle en mouvement après son décollement du site de nucléation.
En appliquant la deuxième loi de Newton, montrer que l'équation différentielle qui régit l'évolution de la vitesse de la bulle s'écrit alors :
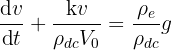
- En déduire l'expression littérale de la vitesse limite vlim atteinte par la bulle.
- L'application numérique donne vlim voisin de 1 mm.s-1. Compte tenu de cette valeur, conclure quant à la validité du modèle proposé.
Prendre des cours de physique chimie permet de progresser en la matière.
2.3. Un autre paramètre à prendre en compte
Les modélisations précédentes ne décrivent pas de manière satisfaisante le mouvement de la bulle dans la boisson gazeuse. En particulier, les expériences réalisées dans du champagne montrent que la variation du volume de la bulle ne peut pas être négligée.
On se propose d'en trouver l'origine.
On suppose que la quantité de matière n0 de gaz présent dans la bulle et la température restent constantes. Dans ce cas, lors d'une remontée de 12 cm du point A à la surface S, la diminution de pression du gaz ne ferait augmenter son volume initial que de 2 %.
Dans la réalité, l'augmentation du volume est un million de fois supérieure ! Un des deux paramètres supposés constants dans le texte précédent ne l'est donc pas.
En s'aidant d'une phrase du texte introductif à la partie 1 de cet exercice, expliquer pourquoi le volume de la bulle augmente si fortement lors de sa remontée.
Durant l'ascension le poids de la bulle est toujours négligeable devant la poussée d'Archimède.
Sachant que le coefficient k défini à la question 2.2. augmente avec le rayon de la bulle, préciser qualitativement l'influence de la variation du volume de la bulle sur chacune des forces qui s'exercent sur elle au cours de la remontée.
Des laboratoires spécialisés ont élaboré des modèles plus satisfaisants tenant compte de paramètres négligés précédemment.
3.L'éclatement des bulles en surface
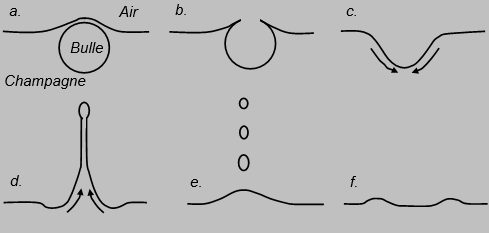
La bulle a maintenant gagné la surface et le film liquide qui constitue la partie émergée de la bulle s'amincit (figure 4.a) jusqu'à se rompre lorsque son épaisseur avoisine le micromètre. Le trou qui apparaît s'ouvre (figure 4.b) et la durée de disparition de la calotte sphérique n'est que de quelques dizaines de microsecondes ! Le cratère qui reste à la surface du liquide ne va pas durer (figure 4.c).
De violents courants apparaissent et, en se refermant, cette cavité projette vers le haut un mince jet de liquide (figure 4.d). Le jet se brise ensuite en fines gouttelettes (figure 4.e) qui en retombant dans le liquide engendrent des ondes circulaires centrées sur la "bulle-mère" (figure 4.f).
Ces observations nécessitent l'utilisation d'une caméra ultra-rapide capable de filmer jusqu'à
2000 images par seconde avec une résolution proche du micromètre (figure 5).

3.1.Malgré l'utilisation de la caméra ultra-rapide, pourquoi ne peut-on pas obtenir d'images du film liquide en train de se rompre ?
3.2. L'onde circulaire créée est-elle longitudinale ou transversale ?Justifier.
Bien qu'éphémère, la vie d'une bulle n'en est pas moins riche en événements !
Prêt pour un cours physique chimie 1ere s ?
Exercice 10
Le canal de Corinthe est situé en Grèce. Il a été creusé pour relier la mer Égée et la mer Ionienne. Les parois rocheuses sont très hautes et l'eau s'écoule à 79 m au-dessous du niveau du sol.
Plusieurs pilotes de moto avaient déjà eu l’intention de franchir le canal de Corinthe, situé en Grèce, mais seul l’Australien Robbie Maddison a réalisé cet exploit en avril 2010.

Il a pris son élan pour accélérer sa moto et atteindre la vitesse de 125 km.h-1. Il a ensuite emprunté une rampe qui lui a permis de franchir le canal, avant d'atterrir de l’autre côté.
Le point le plus haut de son vol a dépassé les 95 mètres au-dessus du niveau de l’eau.

Dans cet exercice on se propose de vérifier les informations sur ce saut à l’aide de cette chronophotographie (photos prises à intervalles de temps identiques).
Le référentiel d’étude est le référentiel terrestre, supposé galiléen pendant la durée du saut.
Le mouvement de Maddison et sa moto est étudié à l'aide du repère (O, x, y) représenté sur la chronophotographie.
À l’instant de date t = 0, Maddison et sa moto se trouvent à l’origine du repère et quittent le tremplin. Le vecteur vitesse du pilote et de sa moto fait alors un angle α avec l’axe horizontal (Ox) comme indiqué sur la chronophotographie.
L’étude est réalisée dans le cadre d’un modèle de chute libre. Maddison et sa moto sont assimilés à un point matériel de masse supposée constante.
Donnée : intensité du champ de pesanteur terrestre, g = 9,81 u.s.i.
1. Pertinence de l’hypothèse d’une chute libre faite par les élèves
Pour justifier que les frottements sont négligeables devant le poids, on étudie le mouvement de Maddison et de sa moto suivant l’horizontale.
1.1 Montrer que si le poids est la seule force qui s’applique sur Maddison et sa moto le mouvement suivant l’axe (Ox) est uniforme. L’établissement des équations horaires du mouvement n’est pas attendu.
Sans souci d’échelle, utiliser l’extrait ci-dessous de la chronophotographie pour valider le modèle de chute proposé. Justifier en précisant les mesures réalisées.

Vérification de la valeur de la vitesse initiale
En tenant compte de l’échelle des distances, on mesure quelques abscisses des positions occupées par Maddison et sa moto et on calcule la vitesse vx suivant l’horizontale pour ces positions. On obtient les valeurs ci-après :
| vx(en m.s – 1 ) | 28,3 | 29,1 | 28,7 | 29,0 | 27,7 | 29,0 |
3. Vérification de la hauteur du saut
En utilisant le modèle de la chute libre et les conditions initiales, on obtient la courbe suivante qui représente la composante suivant y de la vitesse vy(t) en fonction du temps.
3.1 En utilisant l’allure du graphique vy(t), justifier que le mouvement suivant la verticale est uniformément varié.
3.2 Quelle position particulière de la trajectoire est occupée par Maddison et sa moto à la date pour laquelle vy = 0 ? Quelle est alors la valeur de la vitesse à cette date ?
L’énergie potentielle de pesanteur est nulle lorsque y = 0 m.
3.3 Donner l’expression de l’énergie mécanique de Maddison et sa moto en fonction de la masse m, la vitesse v, l’ordonnée y et l’intensité de la pesanteur terrestre g.
3.4 En utilisant l’expression précédente, déterminer l’ordonnée yS du point S, sommet de la trajectoire.
3.5 Le niveau de l'eau du canal de Corinthe est situé à 79 m au-dessous du niveau du sol.
Le point de sortie du tremplin se situe à 5,7 m au-dessus du niveau du sol. Le résultat précédent confirme-t-il l’information suivante : le point le plus haut de son vol a dépassé les 95 mètres au-dessus de l’eau ?
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Je veux vraiment en prendre
Bonjour ! Je vous invite à découvrir nos formateurs passionnés sur Superprof, toujours prêts à vous offrir un accompagnement adapté à vos besoins. Que votre journée soit aussi enrichissante et agréable que possible ! :)
Je voudrais participer
Bonjour, je vous suggère de faire appel à nos professeurs particuliers sur Superprof pour bénéficier d’une assistance sur mesure et approfondie, parfaitement adaptée à vos exigences particulières. Excellente journée à vous ! :)
Quelques exercices sur la masse d’un corps
Bonjour ! Explorez notre équipe de formateurs experts sur Superprof, prêts à vous fournir un accompagnement sur mesure. Belle journée à vous ! :)
Vraiment intéressant
Je suis intéressé
bonjour svp aidé moi à traiter cette exercice
détermine la volume V du caillou
Je retrouve que c’est très bien rédigé c’est parfait pour comprendre
BRAVO 👌👏👍