Chapitres
- 01. Mouvement et énergie
- 02. L'inertie
- 03. Mouvement de l'objet étudié
- 04. La chute libre
- 05. La vitesse
- 06. L'accélération
- 07. Étude de cas
Attention : ce chapitre est limité aux cas où g est constant, donc sur de faibles différences d'altitude et de faible distances horizontales.

Mouvement et énergie

L'énergie est un grandeur difficile à définir, on peut dire cependant que l'énergie caractérise l'état d'un système et exprime la potentialité à modifier l'état d'un autre système avec lequel il est en interaction. L'énergie peut alors se présenter sous différentes formes, dont :
- L'énergie cinétique
- Tout corps en mouvement en possède une. Elle peut être macroscopique : elle dépend alors de la vitesse du corps en mouvement, et donc du référentiel d'étude microscopique : elle est liée à l'agitation moléculaire. Une augmentation de l'énergie cinétique microscopique se traduit par une augmentation de la température.
- L'énergie potentielle
- Elle dépend de la position relative des différentes parties du système: seul un systèmes déformable pourra posséder, à l'échelle macroscopique, de l'énergie potentielle.
L'inertie
En physique, on appelle inertie d'un corps, dans un référentiel galiléen, une tendance de ce corps à conserver sa vitesse. En effet, lorsqu'il y a absence d'influences extérieures, on parle aussi de forces extérieures, alors tout corps que l'on considère comme ponctuel va perdurer dans un mouvement rectiligne uniforme.
Notons que l'on appelle aussi l'inertie, principe d'inertie ou encore loi d'inertie. Puis, lorsque Newton est arrivé, on l'appelle également première loi de Newton.
Elle s'énonce ainsi :
Un système isolé ou pseudo-isolé initialement au repos ou en mouvement rectiligne uniforme demeure dans son état.
On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié.
Même s'il n'existe aucun référentiel galiléen au sens strict. Il est cependant possible de considérer certains référentiels usuels comme galiléen si certaines conditions sont vérifiée :
- Ainsi, le référentiel terrestre peut être considéré galiléen si on considère un mouvement dont la durée ne dépasse pas quelques minutes dans le but de s'affranchir du mouvement de rotation propre de la Terre.
- Le référentiel géocentrique peut également être considéré comme étant galiléen si on considère un mouvement dont la durée ne dépasse quelques heures dans le but de s'affranchir du mouvement de rotation de la Terre autour du Soleil.
- Le référentiel héliocentrique peut aussi être considéré comme étant galiléen car l'impact du mouvement de rotation du Soleil au sein de la galaxie est négligeable.
Où trouver un cours physique chimie ?
Mouvement de l'objet étudié

Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par
rapport auquel on étudiera le mouvement de notre système.
Définition : La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
En simplifiant, on peut définir le référentiel comme quelque chose correspondant au milieu au sein duquel on étudie le mouvement.
En effet, si on choisi de prendre l'exemple du voyageur assit dans un train en marche alors le référentiel vas changer selon l'observateur :
- par rapport à un observateur sur le quai, le voyageur est en mouvement
- par rapport à un observateur dans le train, le voyageur est immobile.
Ainsi, il est possible de conclure que, pour décrire le mouvement d’un mobile, il faut choisir un repère d’espace ou référentiel.
En cours physique chimie lycée, la trajectoire correspond à l’ensemble de toutes les positions successives qu’occupe un point du mobile au cours du temps. La trajectoire peut-être curviligne, c'est à dire en vague, circulaire, donc en forme de rond, ou rectiligne.
- mouvement rectiligne : la trajectoire est une droite
- mouvement circulaire : la trajectoire est un arc de cercle
- mouvement curviligne : la trajectoire est une courbe quelconque, plane ou non.
Deux types de mouvement sont très importants dans l’étude des systèmes :
- la translation : Dans un mouvement de translation, chaque segment de droite, appartenant au mobile, reste parallèle à lui-même, au cours du déplacement et tous les points du mobile ont des trajectoires identiques de même longueur.
- la rotation : Dans un mouvement de rotation, tous les points du mobile décrivent des cercles ou des arcs de cercles centrés sur une droite fixe que l'on appelle axe de rotation. On peut notamment illustrer ce mouvement avec l'exemple des aiguilles d’une horloge.
- Si la trajectoire est une droite, la translation est rectiligne, comme dans le cas d'un ascenseur.
- Si la trajectoire est une courbe, la translation est curviligne, comme dans le cas d'un téléphérique.
- Si la trajectoire est un cercle ou un arc de cercle, la translation est circulaire, comme dans le cas d'une grande roue.
Définition : Une translation correspond à une droite passant par 2 points quelconques du solide qui reste parallèle au cours du mouvement
Définition :Une rotation correspond à un mouvement où tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
Vous cherchez un cours physique chimie 6ème ?
La chute libre

On appelle chute libre le mouvement que prend un objet sous la seule action de son poids.
Un tel mouvement ne peut avoir lieu que dans le vide.
On peut admettre que dans l’air, la chute est " libre " si l’on peut négliger :
- les frottements
- la poussée d’Archimède (il faut que la masse volumique de l’objet soit grande devant celle de l’air).
On a donc une variation du vecteur vitesse du centre d’inertie G de la bille : la valeur de la vitesse varie, la direction reste constante.
On peut monter que pour une hauteur de chute h ( en partant sans vitesse initiale), on a les deux relations suivantes ou v représente la vitesse : 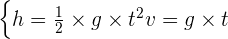
La poussée d’Archimède
La poussée d'Archimède est un phénomène physique qui décrit le comportement de tout corps plongé dans un fluide qu'il soit liquide ou gazeux soumis à un champ de gravité.
Elle est nommée ainsi en l'honneur d'Archimède de Syracuse, un très grand scientifique grec de 200 avant J.-C.
Elle est causée par l'augmentation de la pression du fluide avec la profondeur. Comme la pression exercée sur la partie basse du corps est supérieure à celle exercée sur la partie haute, le corps est poussé verticalement vers le haut.
Voici la formulation d'origine de cette loi physique :
Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée poussée d'Archimède.
Pour que le théorème s'applique il faut que le fluide immergeant et le corps immergé soient au repos. Il faut également qu'il soit possible de remplacer le corps immergé par du fluide immergeant sans rompre l'équilibre.
Voici l'équation qui en résulte :
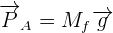
Avec :
- Mf< la masse du fluide contenu dans un volume V et déplacé ;
- g la valeur du champ de pesanteur, de 9,81 N/kg à la surface de la Terre.
La vitesse

La vitesse correspond à une grandeur physique qui est définie par une évolution face au temps.
La vitesse ne définit pas qu’uniquement la vitesse de déplacement mais peut aussi correspondre à la vitesse de réaction chimique ou encore une vitesse de séchage par exemple.
En règle générale, une vitesse est égale à la division de la mesure d’une variation telle qu’une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation.
L’exemple le plus simple est celui de la vitesse de déplacement. Il s’agit d’une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.
Calculer la vitesse
La vitesse est une grandeur qui permet d'exprimer la distance parcourue par le mobile pendant l’unité de temps. La vitesse moyenne est égale au quotient de la distance parcourue par le mobile par la durée de son parcours soit :
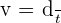 .
.
Avec :
- La vitesse v exprimée en mètre par seconde (m/s) ;
- la distance d exprimée en mètre (m) ;
- Et le temps t exprimé en seconde (s).
Dans le système international (SI), la vitesse cinématique est le mètre par seconde et se note m/s ou m.s-1.
Or, dans le système usuel, on préférera, selon la situation et le mode de transport, le kilomètre par heure qui se note km/h ou km.h-1. En effet, dans la marine, on préférera plutôt le nœud, qui représente 0,5144 m/s.
On trouvera même dans certains cas, dans l'aviation par exemple, le nombre de Mach. Mach 1 est égale à la vitesse du son. Attention, cette vitesse dépend de la température.
Les différents types de vitesse
Rappel concernant l'évolution de la vitesse au cours du temps
Au cours du temps les réactifs disparaissent donc leur concentration diminue. Or nous avons déjà vu que la concentration des réactifs est un facteur cinétique. Plus la concentration des réactifs est faible plus la réaction est lente. Donc, en général, au cours du temps la vitesse de réaction diminue.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est de plus en plus grande, sa vitesse augmente. On dit alors du mouvement qu'il est accéléré.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est constante. On dit que le mouvement est uniforme.
- Si, pour un même intervalle de temps, la distance parcourue est de plus en plus petite, sa vitesse diminue. On dit donc que le mouvement est ralenti.
La vitesse moyenne

La vitesse moyenne se calcule grâce au quotient de la distance L parcourue par la durée T mise à la parcourir. On a donc 
où la longueur de l’arc AB est notée L
La vitesse instantanée
La vitesse instantanée correspond à la vitesse du mobile à l’instant t. Elle peut être assimilé à la vitesse moyenne du mobile durant un intervalle de temps très court dt. On a donc 
Le vecteur vitesse 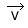
-
- sa direction : celle de la tangente à la trajectoire en M
- son sens : celui du mouvement
- sa valeur : valeur de la vitesse instantanée à l’instant t
- son origine : le point M
Notons qu'il est possible de la calculer grâce à la formule suivante 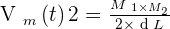
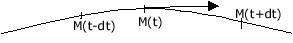
- Lors d'un mouvement rectiligne uniforme, me vecteur vitesse d’un point mobile est constant. Sa valeur, sa direction et son sens restent les mêmes à chaque instant..
- Lors d'un mouvement rectiligne varié, le vecteur vitesse garde la même direction mais les distances parcourues par le point mobile pendant des durées égales sont différentes.
- Une trajectoire correspond à un cercle dont le plan est orthogonal à l’axe fixe
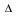
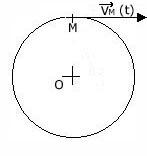
- La vitesse angulaire moyenne se définit ainsi : Soit un point M décrivant une trajectoire circulaire de rayon R. Un rayon du cercle balaie un angle
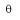
La vitesse angulaire moyenne peut se calculer grâce à l'expression suivante 
- La vitesse angulaire instantanée correspond à la vitesse angulaire à un instant donné. C’est le quotient du petit angle d θ balayé par un temps très court dt :
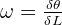 avec ω en rad/sd et θ en raddt en s
avec ω en rad/sd et θ en raddt en s
Il est tangent à la trajectoire au point considéré donc perpendiculaire au rayon. Son sens est celui du mouvement. Sa valeur est celle de la vitesse linéaire instantanée en ce point.
Le point M décrit un arc AB pendant la durée t. Le rayon OM = R balaie l’angle q. Donc l’arc AB est égal à rq.
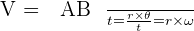
- La période, notée T, est l’intervalle de temps séparant 2 passages du mobile au même point et dans le même sens :
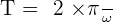 . La période s’exprime en seconde et la vitesse angulaire en rad/s
. La période s’exprime en seconde et la vitesse angulaire en rad/s - La fréquence, notée f, est le nombre de tours effectués par le mobile en une seconde :
 . La fréquence s’exprime en Hertz (Hz).
. La fréquence s’exprime en Hertz (Hz).
L'accélération
L'accélération correspond à un phénomène attenant à l'augmentation de la vitesse. L'accélération est égale à la dérivée de la vitesse instantanée. C'est à dire que la fonction dérivée de la fonction qui détermine la position d'un point selon le temps est l'accélération.
Il s'agit d'une grandeur physique qui s'exprime sous la forme de vecteur. Comme la vitesse, il s'agit d'une variation au cours du temps.
La norme de ce vecteur est l'accélération. Selon le système international, l'accélération a pour unité le mètre par seconde carré qui se note m.s-2.
Les débuts de cette notion
C'est en 1700 qu'un père jésuite français, Pierre Varignon, commence à identifier l'existence de l'accélération dans ces calculs. En effet, ce mathématicien a été l'un des premiers à chercher à comprendre le principe de la vitesse.
Approche graphique
Lors d'un courbe d'accélération, quand la vitesse est maximale, l'accélération est minimale.
Calculs
On peut effectuer différents calculs sur l'accélération. Voici ceux que vous pourriez être amenés à effectuer.
Accélération moyenne
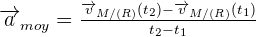
Accélération instantanée
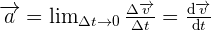
Étude de cas
Mouvements de chute libre
On appelle chute libre le mouvement d'un objet soumis seulement à son poids (pas de frottements). En théorie, ce cas n'est applicable qu'aux mouvements dans le vide, mais dans la pratique, on néglige la résistance de l'air (pour des objets à bonne pénétration aérodynamique, ou de faibles dimensions).
- Système : le solide soumis à son poids.
- Référentiel : terrestre supposé galiléen.
- Le solide est soumis à son poids P.
- P = m.g
D’après la deuxième loi de Newton en projection sur un axe vertical, orienté vers le bas : [ m a = P = m g ]
L'accélération ne dépend donc pas de la masse de l'objet considéré, ni de la manière dont il est lancé (vitesse initiale).
Chute libre verticale
Sans vitesse initiale
Il est évident que, si on lâche un objet (sans le pousser ou le jeter), il tombe verticalement ! De plus, comme a = g, l'accélération est constante, le mouvement est donc uniformément accéléré.
Choisissons deux axes, celui des z (verticalement, orienté vers le haut) et celui des x (horizontalement). On prend l'origine du repère au temps t = 0 s, où l'objet est lâché.
A t0 = 0 s, on a donc vx = 0 et vz = 0.
A un temps t quelconque, on a : [ az = - g ]
On intègre et on trouve : 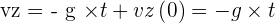 (la vitesse initiale est nulle).
(la vitesse initiale est nulle).
Encore une intégration : 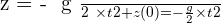 (car z(0) = 0).
(car z(0) = 0).
Avec une vitesse initiale verticale
Cette fois v(0) n'est pas nulle
Les équations horaires deviennent donc :
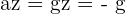

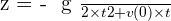
Chute libre avec une vitesse initiale quelconque
On tire un projectile de masse m, à la date t = 0 s, avec une vitesse initiale v0 faisant un angle b avec l'horizontale. On étudie la trajectoire dans le plan (Ox,Oz), qui contient v0 : c'est le plan de tir.
Équations horaires
Comme d'habitude, a = g, donc ax = 0 et az = - g.
Donc : 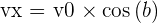 et
et 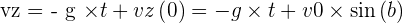
Mais encore :  et
et 
Remarques :
Si v0 = 0 (vecteur nul), alors x = 0, c'est une chute libre.
Si b = ± 90 degrés alors x = 0, il s'agit d'une chute verticale avec vitesse initiale.
Allure de la trajectoire
Des équations horaires, on tire 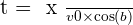 , que l'on remplace dans z :
, que l'on remplace dans z :
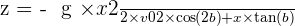
C'est l'équation de la trajectoire du projectile, et c'est une parabole, comme pour tous les mouvements de chute libre.
Portée de tir
On appelle P le point où le projectile atteint le sol, la distance OP (avec O point du lancer) étant alors dénommée " portée de tir ".
Si l’altitude de référence 0 à été prise au niveau du sol (c'est-à-dire si le lancer s'effectue du sol), alors on prend l'équation de la parabole et on résout z = 0. Dans notre cas, 
Autre question : quelle est la vitesse en P ? C'est v0, car la différence d'énergie cinétique est nulle (travail du poids nul entre deux points de même altitude) !
Hauteur maximale atteinte
Appelons S le point d'altitude maximale de la trajectoire : S est alors appelée " flèche " de la trajectoire. Comment déterminer les coordonnées de S ?
On résolvant l'équation vz = 0, on peut trouver la date à laquelle le projectile passe au point S, et calculer ensuite z et x.
S, le sommet de la parabole, a pour coordonnée horizontale celle du milieu de [OP].
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Moi je le trouve intéressant