Chapitres

Généralités sur les ondes
Définitions
Une onde mécanique progressive est la propagation d’une perturbation dans un milieu matériel, sans transport de matière mais avec transport d’énergie. Onde transversale : Onde pour laquelle la matière est momentanément déplacée dans une direction perpendiculaire à la direction de la propagation. 

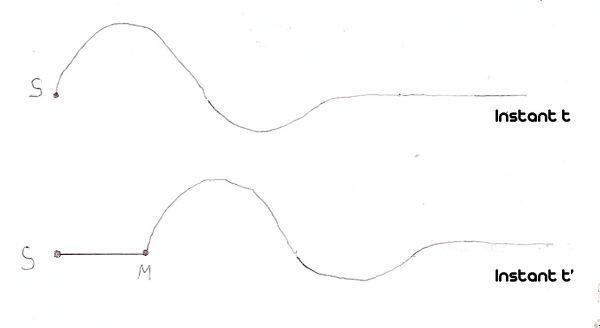
Caractéristiques
Une onde se propage dans toutes les directions qui lui sont offertes. L’onde se propage de proche en proche. Certaines ondes ont besoin d'un milieu matériel pour se transmettre. C'est le cas par exemple des ondes sonores qui seraient incapables de se propager dans le vide. 
Les fréquences des ondes
Les signaux à transmettre usuellement, comme par exemple les sons (voix des pilotes, des contrôleurs aériens), sont constitués d’ondes de basses fréquences. Leur faible distance de propagation, la superposition d’un grand nombre de ces signaux dans l’environnement et le fait que les dimensions des antennes réceptrices doivent être de l’ordre de grandeur de la longueur d’onde des signaux à capter, constituent autant d’obstacles à leur utilisation directe. La modulation est alors une solution pour transmettre les signaux : on fait varier l’une des caractéristiques (amplitude, fréquence…) d’un signal de fréquence beaucoup plus élevée (porteuse), avec l’information à transmettre (signal modulant). On obtient un signal modulé.
Périodicité
On parle de périodicité dans le cas d'une onde mécanique progressive. Une période est un temps qui se mesure habituellement en secondes. Elle représente le temps qui s'écoule entre deux moments identiques de l'onde. Une fois qu'on connait la période, on peut facilement définir la fréquence de l'onde. Celle-ci est égale à l'inverse de la période.
Exercices d'application
Exercice 1 : Ondes et particules
Si l’on parvient à établir la correspondance entre ondes et corpuscules pour la matière, peut-être sera-t-elle identique à celle qu’on doit admettre entre ondes et corpuscules pour la lumière ? Alors on aura atteint un très beau résultat : une doctrine générale qui établira la même corrélation entre ondes et corpuscules, aussi bien dans le domaine de la lumière que dans celui de la matière. D’après Notice sur les travaux scientifiques, de Louis de Broglie, 1931
Données numériques
Masse d’un électron : me = 9,1 × 10-31 kg Charge élémentaire : e = 1,6 × 10-19 C Constante de Planck : h = 6,6 × 10-34 J.s Vitesse de propagation de la lumière dans le vide : c = 3,0 × 108 m.s-1
Partie A : Expérience des fentes d’Young

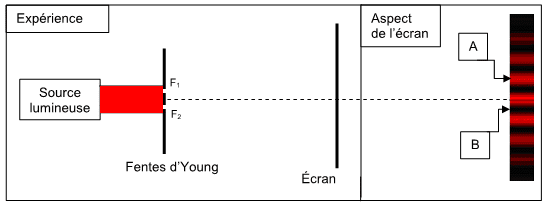
Partie B : Particule de matière et onde de matière
1. Expérience des fentes d’Young En 1961, Claus Jönsson reproduit l’expérience des fentes d’Young en remplaçant la source lumineuse par un canon à électrons émettant des électrons, de mêmes caractéristiques, un à un. L’impact des électrons sur l’écran est détecté après leur passage à travers la plaque percée de deux fentes. Répondre aux questions suivantes à partir des documents 1 et 2. 1.1. Peut-on prévoir la position de l’impact d’un électron ? Justifier. 1.2. En quoi cette expérience met-elle en évidence la dualité onde-particule pour l’électron ? Détailler la réponse. 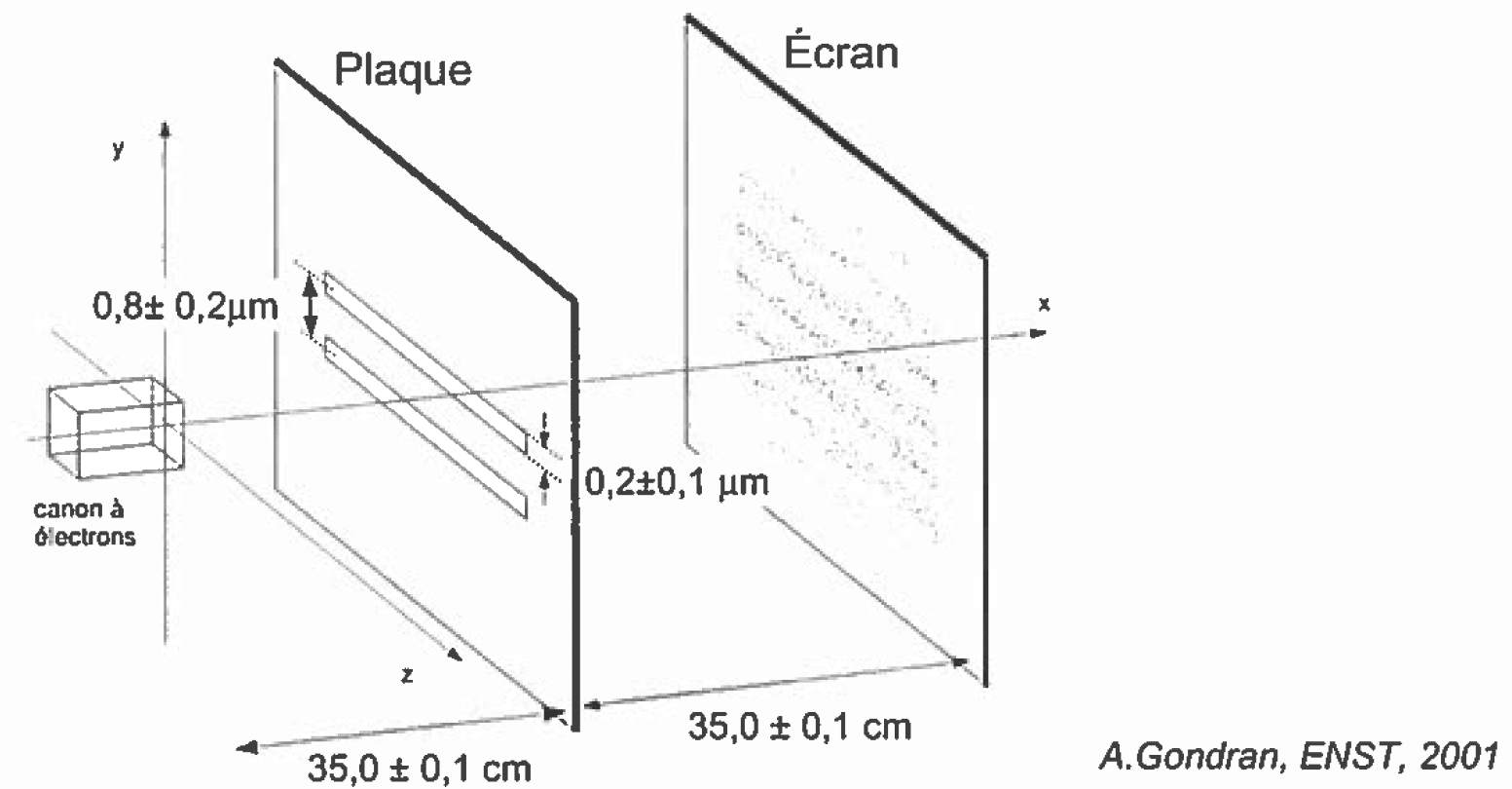
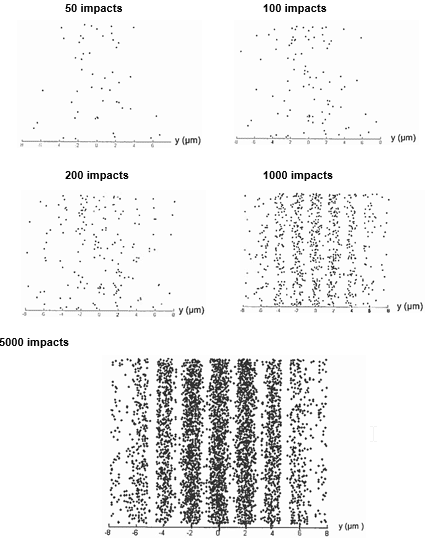
- L’interfrange est donnée par la relation : où i est l’interfrange, λ la longueur d’onde de l’onde associée à un électron, D la distance entre la plaque et l’écran et b la distance séparant les deux fentes. Toutes ces grandeurs s’expriment en mètres ;
- Incertitude sur la mesure de l’interfrange : Δi = 0,2 µm ;
- Vitesse des électrons : v = 1,3 × 108 m.s-1.
2.1.1. Déterminer la valeur de la longueur d’onde de l’onde de matière associée à un électron et donnée par la relation de de Broglie. On admettra que cette valeur est connue avec une incertitude égale à 5 × 10–13 m. 2.1.2. Vérifier la cohérence des observations expérimentales réalisées avec le résultat précédent. 2.2. Passage à travers une seule fente de la plaque L’une des deux fentes de la plaque est dorénavant bouchée ; l’autre de largeur a = 0,2 µm est centrée sur l’axe Ox du canon à électrons. 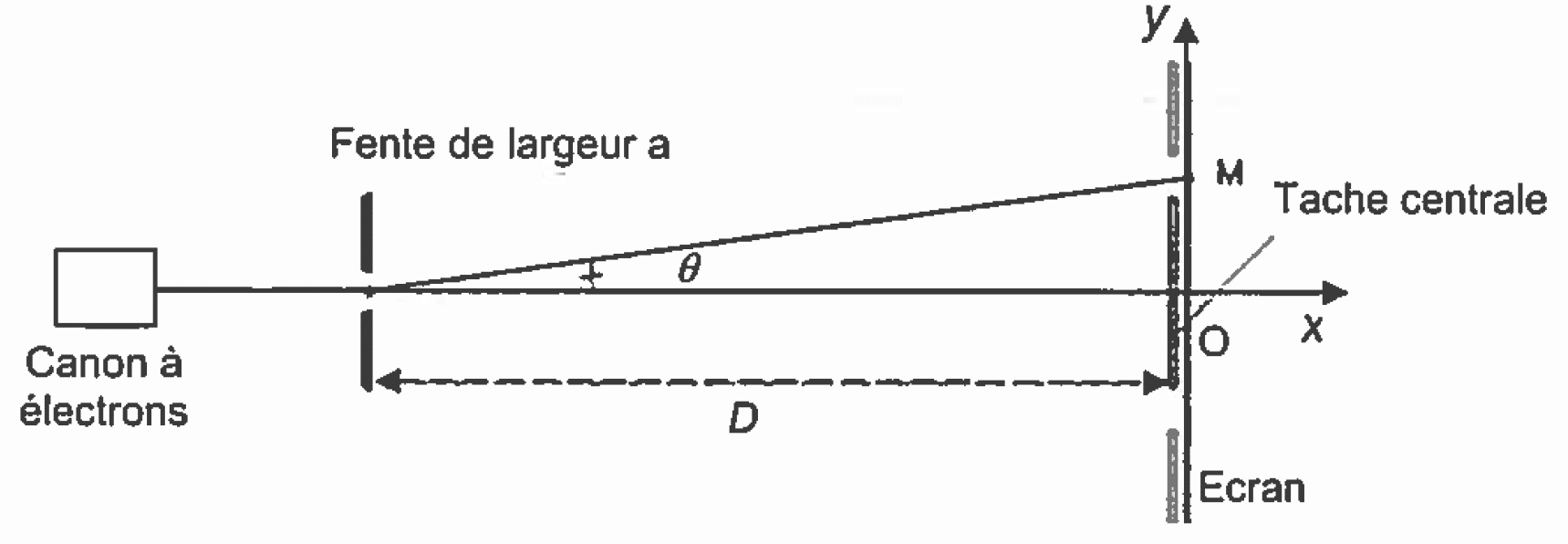

passage par la fente.
Exercice 2 : Questions sur les ondes
Les questions sont indépendantes Répondre aux questions suivantes en justifiant toutes vos réponses.
Question 1
On excite l’extrémité d’une corde à une fréquence de 50 Hz. Les vibrations se propagent le long de la corde avec une célérité de 10 m.s-1. Quelle est la longueur d’onde ?
Question 2
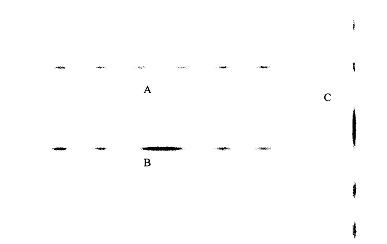
Un faisceau de lumière, parallèle monochromatique, de longueur d’onde l, arrive sur une fente horizontale de largeur a (a est de l’ordre du dixième de millimètre). Quelle figure de diffraction parmi celles proposées dans l’annexe, schéma 1, observe-t-on sur l’écran situé à une distance D, grande devant a.
Question 3
- La fréquence d’une radiation lumineuse monochromatique, qui passe d’un milieu transparent à un autre milieu d’indice plus élevé, ne change pas.
- La longueur d’onde d’une radiation lumineuse monochromatique, qui passe d’un milieu transparent à un autre milieu d’indice plus élevé, ne change pas.
Ces affirmations sont-elles vraies ou fausses ?
Question 4
4.1. La célérité du son diminue-t-elle quand la température augmente ? 4.2. La célérité du son varie-t-elle avec la fréquence ? 4.3. La célérité du son dans l’air est-elle de l’ordre de 1000 km.s-1 ?
Question 5
Un pêcheur à la ligne est au bord d’un lac tranquille. Soudain un enfant vient perturber la surface de l’eau en jetant un caillou à quelques mètres du flotteur. Le flotteur se déplace-t-il à la célérité v de l’onde ? 
Question 6
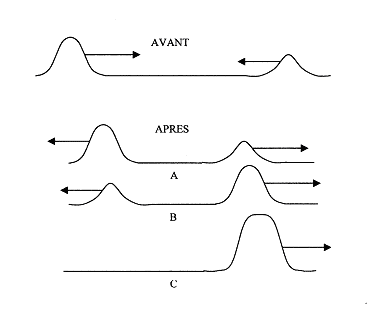
Deux ébranlements se propagent en sens contraire sur une corde tendue. On a représenté (annexe schéma 2) plusieurs situations possibles après leur point de rencontre. Choisir celle qui est physiquement possible.
Annexes
Exercice 3 : Les ondes gravitationnelles
Clin d’œil de l’histoire : c’est 100 ans tout juste après la publication de la théorie de la relativité générale d’Einstein, qu’une équipe internationale en a confirmé l’une des prédictions majeures, en réalisant la première détection directe d’ondes gravitationnelles. 
Données
- Masse du Soleil : MS = 2,00 x 1030 kg ; - Les ondes gravitationnelles se propagent à la célérité de la lumière dans le vide, soit c = 3,00x 108 m.s-1 ; - Constante de gravitation universelle : G = 6,67 x 10-11 m3.kg-1.s-2. 1. Les ondes gravitationnelles détectées 100 ans après la prédiction d’Einstein Pour la première fois, des scientifiques ont observé des ondes gravitationnelles, produites par la collision de deux trous noirs. Cette découverte confirme une prédiction majeure de la théorie de la relativité générale énoncée par Albert Einstein en 1915. Ces ondes ont été détectées le 14 septembre 2015 par les deux détecteurs jumeaux de LIGO (Laser Interferometer Gravitational-wave Observatory) situés aux États-Unis à Livingston, en Louisiane, et à Hanford dans l’État de Washington, distants de 3000 km. L’analyse des données a permis d’estimer que les deux trous noirs ont fusionné il y a 1,3 milliard d’années et qu'ils avaient des masses d’environ 29 et 36 fois celle du Soleil. Selon la théorie de la relativité générale, un couple de trous noirs en orbite l’un autour de l’autre perd de l’énergie sous forme d’ondes gravitationnelles, ce qui entraîne un rapprochement des deux astres. Ce phénomène peut durer des milliards d’années avant de s’accélérer brusquement. En une fraction de seconde, les deux trous noirs entrent alors en collision et fusionnent en un trou noir unique. Une énergie colossale est alors convertie en ondes gravitationnelles. C’est cette "bouffée" d’ondes qui a été observée. D’après le communiqué du CNRS - 11 février 2016 1.1. À quelle distance de la Terre, exprimée en année-lumière, se trouve la source des ondes gravitationnelles détectées le 14 septembre 2015 ? 1.2. Le détecteur de Livingston a détecté les ondes gravitationnelles 7 ms avant celui de Hanford. Cet écart a permis d’envisager des localisations possibles de leur source. 
ondes gravitationnelles.
noirs de même masse.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !