Chapitres

Définition
Le circuit RCL est un circuit électrique qui se compose toujours d'au moins trois éléments :
- Une résistance ;
- Une bobine ;
- Un condensateur.
Ces circuits peuvent être montés en parallèle ou en série. Le but de ces circuits et d'en observer les résonances résultantes à l'injection d'oscillations.

Quelques calculs sur les différents phénomènes
Décharge d'un condensateur dans une bobine
Régime pseudo périodique
UC passe par un maximum à intervalle de temps régulier mais l'amplitude diminue. C'est la résistance totale du circuit qui est responsable de l'amortissement des oscillations.
Régime critique
Si la résistance devient trop importante, les oscillations disparaissent. On passe d'un régime pseudo périodique à un régime critique. Si on a un régime critique la tension aux bornes du condensateur diminue très rapidement jusqu'à 0.
Régime apériodique
Il est l'équivalent d'une décharge classique 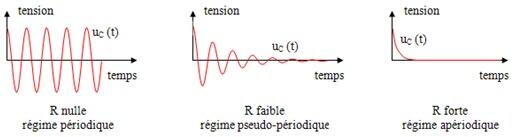
Expression de la pseudo-période
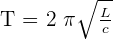
Équation différentielle d'un circuit RLC en régime libre
Loi d'additivité des tensions


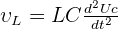

La loi d'Ohm
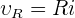

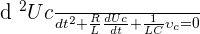
Oscillations non amorties d'un circuit LC
Équation différentielle d'un circuit LC
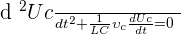
Solution de l'équation différentielle
La solution est de la forme : UC = UM \cos (ω0t + φ)
Détermination de φ et UM
UC avec t= 0, U =E Faire la dérivée de U puis la remplacer dans la formule de I(t) i(t) avec t=0, on obtient φ = 0 Conclure que UM = E ð UC = E \cos(ω0t)
Expression de T0
Prendre l'équation différentielle Dériver la solution de cette équation Trouver la dérivée seconde de cette solution Remplacer dans l'équation différentielle  où :
où : 

Aspect énergétique
Energies
ETOT = EC + EL ð ETOT = ½ CE² L'énergie totale se conserve si on néglige les résistances du circuit. Il y a un transfert d'énergie entre la bobine et le condensateur.
Oscillations amorties
Le responsable des amorties est la résistance. Dans les cas d'oscillations amorties, il y a pertes d'énergie par effet Joule dû à la résistance. Il est rendu sous forme d'énergie thermique.
Les composants du circuit RLC
Les condensateurs
La définition d'un condensateur
Un condensateur est un composant en électronique qui a la capacité de stocker de l'énergie électrique. Il stocke cette électricité en fonction de la tension qu'il reçoit et ce de manière proportionnelle.
Les marques du condensateur
Selon sa capacité, un condensateur reçoit un marquage signifiant sa valeur. La plupart du temps, le marquage respecte le schéma suivant XXY dans lequel la partie XX correspond à la valeur et Y à la puissance de 10 en picofarads de symbole pF. Par exemple 122 correspondra à 12 x 102 pF. Il peut aussi arrivé que l'on voit juste une valeur à deux chiffres. Il s'agit dans ce cas d'un marquage d'une valeur en microfarads de symbole µF. Pour finir, quand les condensateurs sont assez gros et laissent la place pour une inscription complète, on retrouve la valeur ainsi que son unité directement marqués sur le condensateur en question.
La modélisation du condensateur
Pour modéliser un condensateur, il faut décrire certaines de ses caractéristiques à savoir la résistance, l'inductance, la valeur de la capacité et parfois l'effet de batterie ou encore l'hystérésis de charge du condensateur.
Les usages du condensateur
Les usages du condensateur

Les condensateurs sont utilisés dans moult domaines.
Stabilité
Les condensateurs peuvent être utilisés dans des installations électriques afin de "lisser" la tension d'un circuit. Dans ces conditions, le condensateur se chargera lors des pics de tension tout en se relâchant lors des baisses de tension. Cette dernière ne subissant pas de fluctuations du point de vue des appareils électriques du circuit et ainsi de leurs utilisateurs. Ils sont donc présents dans de nombreux appareils ménagers que vous possédez chez vous :
- Plaques de cuisson ;
- Radiateurs ;
- Chauffe-eau ;
- Ordinateur ;
- Bouilloire ;
- Sèche cheveux.
Séparer les courants
On peut utiliser les condensateurs afin de séparer deux courants qui seraient présents simultanément : le courant alternatif et le courant continu. En effet, le courant continu ne peut passer à travers un condensateur car il ne se vide que quand sa capacité maximale est atteinte et ne peut donc pas délivrer le courant de façon continu.
Traiter les signaux
Les condensateurs sont capables de filtrer des signaux périodiques. Par exemple, dans une radio, le condensateur peut filtrer le signal sinusoïdale périodique de la radio FM.
Stocker
Dans le cas des super condensateurs, il peuvent être utilisés afin de stocker de l'énergie. En effet, leur grande capacité leur permet de retenir beaucoup d'énergie.
La résistance
Définition d'une résistance
La résistance désigne la capacité physique d'un matériau à s'opposer au passage d'un courant électrique sous une certaine tension. C'est de là que sont nés les composants électriques appelés les résistances.
Notations
Une résistance est habituellement représentée par un rectangle et se note R, K ou M selon sa capacité. R représente les ohms, K les kiloohms et pour finir, M les Megohms.
Composition
Une résistance peut-être composée de divers matériaux selon qu'elle soit de faible ou haute puissance. Par exemple, les résistances de moins de 2 W sont constituées de carbone et de céramique. Ce type de résistance a pour avantage de générer très peu de bruit thermique, ce qui en fait un élément de choix dans les On retrouve aussi lescircuits audio. Les résistances faites pour supporter des puissances supérieures seront quand à elles fabriquées à l'aide d'un cylindre de céramique sur lequel sera enroulé un fil conducteur. Pour finir, les résistances à très hautes puissance sont constituées de solution aqueuse contenant des ions cuivre et qui ralentissent grandement le passage du courant électrique.
La bobine
Une bobine est un composant électrique dont la fonction est de s'opposer au passage du courant.
Notation
Comme sur les résistances, il existe un code couleur pour connaître la valeur des bobines. Voici un tableau qui les détaille :
| Couleur | Premier anneau | Deuxième anneau | Anneau multiplicateur |
|---|---|---|---|
| Argent | 10−2 µH | ||
| Or | 10-1 µH | ||
| Noir | 0 | 0 | 1> µH |
| Marron | 1 | 1 | 101 µH |
| Rouge | 2 | 2 | 102 µH |
| Orange | 3 | 3 | 103 µH |
| Jaune | 4 | 4 | 104 µH |
| Vert | 5 | 5 | 105 µH |
| Bleu | 6 | 6 | 106 µH |
| Violet | 7 | 7 | 107 µH |
| Gris | 8 | 8 | 108 µH |
| Blanc | 9 | 9 | 109 µH |
Composition
Une bobine se compose d'un enroulement de fil conducteur, généralement à base de cuivre, autour duquel sont assemblées des feuilles de fer conducteur.

Utilisations
On utilise les bobines dans de nombreuses fonctions du quotidien. Par exemple, on retrouve les bobines dans les voitures, dans la bobine d'allumage. Cet organe du moteur a pour fonction de produire une grande quantité d'énergie. On les retrouve donc dans le circuit des bougies d'allumage afin de fournir les étincelles nécessaires à l'allumage des cylindres. On retrouve aussi les bobines dans les éléments électromagnétiques. En effet, la bobine a de grandes capacités pour les électroaimants et relais électromécaniques. On peut aussi les rencontrer parfois dans les filtres de signal électrique. Ils peuvent réduire l'ondulation résiduelle ou les fréquences parasites.
Exercices d'application
Problème 1 : Résonance d’un dipôle RLC parallèle
Etude d’un dipôle en régime sinusoïdal forcé de pulsation ω
On considère entre deux points A et B. le circuit comportant en parallèle : une résistance R, une Inductance pure L, un condensateur de capacité C. Ecrire l’expression de l'admittance complexe Y du dipôle AB en fonction de R, L, C, et ω. On pose 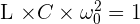
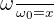 et
et  Exprimer ( Y , R ) sous la forme 1 + j . g ( x , Q ) où f ( x , Q ) désigne une fonction simple de x et de Q. En déduire l’expression de l’Impédance complexe Z du dipôle AB. Préciser le comportement de ce dipôle aux basses fréquences et aux hautes fréquences : on donnera une interprétation physique du dipôle équivalent obtenu. Etudier brièvement le comportement en fonction de x du module de Z : tracer l'allure de la courbe représentative.
Exprimer ( Y , R ) sous la forme 1 + j . g ( x , Q ) où f ( x , Q ) désigne une fonction simple de x et de Q. En déduire l’expression de l’Impédance complexe Z du dipôle AB. Préciser le comportement de ce dipôle aux basses fréquences et aux hautes fréquences : on donnera une interprétation physique du dipôle équivalent obtenu. Etudier brièvement le comportement en fonction de x du module de Z : tracer l'allure de la courbe représentative.
Utilisation du dipôle précédent
On alimente le dipôle précédent AB par une source de tension alternative sinusoïdale 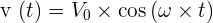 On associe à l’Intensité Instantanée dans le dipôle AB
On associe à l’Intensité Instantanée dans le dipôle AB  l’Intensité complexe [ I = I _ 0 \times e ^ { j \times \phi } ] On néglige l’impédance Interne du générateur. Ecrire, sans démonstration, l’expression de I en fonction de V0 , R, Q et x. On note l le module de I : quel est l’ensemble des valeurs do x tel que
l’Intensité complexe [ I = I _ 0 \times e ^ { j \times \phi } ] On néglige l’impédance Interne du générateur. Ecrire, sans démonstration, l’expression de I en fonction de V0 , R, Q et x. On note l le module de I : quel est l’ensemble des valeurs do x tel que 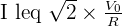 : montrer que cet ensemble est limité par deux valeurs x2 et X1 et calculer x2 - x1. en fonction de Q. Etudier brièvement le déphasage \phi de l’Intensité I ( t ) par rapport à la tension u ( t ) en fonction de x. Tracer U courbe φ(x). Calculer pour x = 0,9 ; L = l * m * H ; C = 0.1 µF et R = 500 Ω les valeurs numériques de phi, de x2 – x1 et de Q. On choisit ω = ω0 Quelles sont en notation complexes les expressions des intensités dans les branches comportant L et C ? Ecrire également les expressions des intensités Instantanées. Que constate-t*on 7 Quel nom pourrait-on donner au coefficient Q.
: montrer que cet ensemble est limité par deux valeurs x2 et X1 et calculer x2 - x1. en fonction de Q. Etudier brièvement le déphasage \phi de l’Intensité I ( t ) par rapport à la tension u ( t ) en fonction de x. Tracer U courbe φ(x). Calculer pour x = 0,9 ; L = l * m * H ; C = 0.1 µF et R = 500 Ω les valeurs numériques de phi, de x2 – x1 et de Q. On choisit ω = ω0 Quelles sont en notation complexes les expressions des intensités dans les branches comportant L et C ? Ecrire également les expressions des intensités Instantanées. Que constate-t*on 7 Quel nom pourrait-on donner au coefficient Q.

Problème 2 : calculs d’impédance
Soit le dipôle A B constitué d'une résistance R et d'une bobine d'inductance L associées en parallèle. Soit le dipôle A‘ B‘ constitué d'une résistance R' et d'une bobine d'inductance L' associées en série. Ces deux dipôles sont soumis A une tension sinusoïdale de pulsation ω. Déterminer R' et L' en fonction de R , L et ω pour que, à la pulsation ω , ces dipôles soient équivalents . Quelle est alors la pulsation ω0 pour laquelle on a :  Calculer ω0 pour R = 102 Ω et L = 10-2 H On considère le montage auquel on applique entre les bornes A et C du dipôle une tension de la forme :
Calculer ω0 pour R = 102 Ω et L = 10-2 H On considère le montage auquel on applique entre les bornes A et C du dipôle une tension de la forme : 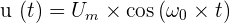 Les dipôles A B et B C étant équivalents et la pulsation ω0 étant telle que :
Les dipôles A B et B C étant équivalents et la pulsation ω0 étant telle que :  Dans cette partie, on écrira les expressions demandées de la façon la plus simple possible en tenant compte des hypothèses. Déterminer l'Impédance complexe ZAC du dipôle. Le résultat sera exprimé sous forme polaire
Dans cette partie, on écrira les expressions demandées de la façon la plus simple possible en tenant compte des hypothèses. Déterminer l'Impédance complexe ZAC du dipôle. Le résultat sera exprimé sous forme polaire 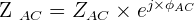 Donner l'expression du courant total i (t ) en fonction du temps . Calculer en fonction de la représentation complexe u de u ( t ) les expressions complexes u1 et u2 des tensions aux bornes de A B et de B C. Déterminer les représentations complexes i1 et i2 des Intensités i1 ( t ) dans R et i2 ( t ) dans L . En déduire les valeurs efficaces de u1 ( t ) ; u2 ( t ) ; i1 ( t ) et i2 ( t ) ainsi que leurs déphasages par rapport à u ( t ). Donner l'expression de la capacité C qu'il faut mettre en série avec le dipôle A C pour que le courant total i ( t ) soit en phase avec u ( t ) à la pulsation ω0 . Calculer C avec les données numériques précédentes.
Donner l'expression du courant total i (t ) en fonction du temps . Calculer en fonction de la représentation complexe u de u ( t ) les expressions complexes u1 et u2 des tensions aux bornes de A B et de B C. Déterminer les représentations complexes i1 et i2 des Intensités i1 ( t ) dans R et i2 ( t ) dans L . En déduire les valeurs efficaces de u1 ( t ) ; u2 ( t ) ; i1 ( t ) et i2 ( t ) ainsi que leurs déphasages par rapport à u ( t ). Donner l'expression de la capacité C qu'il faut mettre en série avec le dipôle A C pour que le courant total i ( t ) soit en phase avec u ( t ) à la pulsation ω0 . Calculer C avec les données numériques précédentes.
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Suis satisfait
J’ai apprécié
Merci ! :)