Chapitres

Les principes de l'écoulement
L'écoulement laminaire
Quand on parle d'écoulement laminaire en mécanique des fluides, on évoque le mode d'écoulement d'un fluide dans le cas où l'ensemble du fluide s'écoule plus ou moins dans la même direction et cela sans que les différences locales ne se contrarient. On est alors en opposition au régime turbulent au cours duquel l'écoulement produit des tourbillons qui vont mutuellement se contrarier.

Ainsi, lorsque l'on cherche à faire circuler un fluide dans un tuyau, on cherche à mettre en place un écoulement laminaire afin qu'il y ait moins de pertes de charge. Mais on cherche aussi à mettre en place un écoulement laminaire lorsque l'on cherche à faire voler un avion afin que le vol soit stable et prévisible à l'aide d'équations. Lorsque l'on observe un écoulement laminaire à l'échelle microscopique, on peut observer que deux particules de fluides qui sont voisines à un instant défini resteront voisines lors des prochains moments d'observation. De par cette observation, on peut décrire un champ de vitesse grâce à l'utilisation de techniques classiques d'analyse mathématique. Dans le cas où l'écoulement devient turbulent, celui-ci devient alors sans organisation apparente. Les techniques classiques d'analyse mathématique utilisées précédemment ne suffisent alors plus pour décrire le champ de vitesse. Tout comme la notion de régime turbulent, la notion de régime laminaire est très fortement liée à la viscosité du fluide en mouvement. En effet, lorsque le liquide se situe dans une conduite ou autour d'un obstacle, alors, au voisinage d'une paroi sur laquelle la vitesse relative du fluide est nulle, on peut alors observer l'apparition de fortes variations de vitesse au sein desquelles la viscosité est impliquée. De façon plus précise, on peut dire que l'écoulement visqueux est caractérisé grâce à un nombre sans dimension que l'on appelle le nombre de Reynolds. Ce nombre permet alors de mesurer l'importance relative des forces inertielles qui sont liées à la vitesse et des forces de frottement qui sont liées à la viscosité. Ainsi, si ces dernières sont prépondérantes, alors on peut dire que le frottement, qui se produit entre deux couches de fluides, maintient leur cohésion : on obtient ainsi un écoulement laminaire. Dans le cas où le nombre de Reynolds augmente au-delà d'un certain seuil, alors l'écoulement est déstabilisé. Dans ce cas, il peut y avoir un régime turbulent qui va se mettre en place après qu'une phase de transition, plus ou moins importante, ait eu lieu. Puisque la viscosité de l'air est beaucoup plus faible que la viscosité de l'eau, on peut alors conclure que son effet est, par la même façon, plus faible et ne se limite qu'à la zone proche de la paroi dans laquelle on peut observer que la vitesse varie forcement. On appelle alors cette zone d'effet la couche limite. Ainsi, lorsque l'on se situe à une distance suffisante de la paroi, on peut observer que les variations deviennent suffisamment faibles pour que l'on puisse négliger la viscosité. De ce fait, on peut considérer le fluide comme étant parfait lorsqu'il se situe autour de l'obstacle auquel on ajoute la couche limite. A cela il est possible d'ajouter que, au bord d'attaque d'une aile, puisque la vitesse relative est nulle, la viscosité reste sans effet. La couche limite laminaire fini par devenir une couche turbulente. Néanmoins, la partie de cette couche proche de la paroi constitue un film laminaire.
Le nombre de Reynolds
Le nombre de Reynolds, noté Re, correspond à un nombre sans dimension qui est utilisé en mécanique des fluides. Cette grandeur permet alors de caractériser un écoulement, en particulier la nature de son régime. Il est ainsi possible de savoir si un écoulement est laminaire, transitoire ou turbulent.
Le régime turbulent
Le terme turbulence correspond à l'état de l'écoulement d'un fluide, qu'il soit liquide ou gaz, au sein duquel la vitesse présente un caractère tourbillonnaire. On entend par là la présence de tourbillons dont la taille, la localisation mais également l'orientation vont, de façon constante, varier.

On peut caractériser un écoulement turbulents par une apparence très désordonnée mais également par un comportement qui restera difficilement prévisible et par l'existence de nombreuses échelles spatiales et temporelles. Il est possible de voir apparaître ce type d'écoulement dans le cas où la source d'énergie cinétique, qui provoque la mise en mouvement du fluide, est relativement intense devant les forces de viscosité que le fluide va opposer pour se déplacer. On peut alors opposer cet écoulement au régime laminaire qui est régulier. Pour étudier le comportement complexe des écoulements turbulent, il faut, dans la plupart des cas, utiliser la voie statistique. En effet, on peut, de ce fait, considérer que cette étude fait partie intégrante de la physique statistique afin de traduire que, lors d'un écoulement, les forces d'inertie l'emportent sur les forces de viscosité.
La perte de charge
La perte de charge est un phénomène qui intervient en mécanique des fluides. C'est pourquoi un fluide en mouvement perd son énergie mécanique par dissipation à cause des frottements. Pour calculer la perte de charge, on utilise le théorème de Bernoulli.
Le théorème de Bernoulli
Le théorème de Bernoulli est une théorème physique qui a été énoncé en 1738 par Daniel Bernoulli. Il parle des mouvements des fluides, d'hydrostatique et de dynamique des fluides. On en retire notamment que la vitesse augmente en cas de baisse de pression sur un fluide homogène et incompressible. Aujourd'hui, ce théorème est fortement utilisé dans l'aérodynamique afin de régler des problèmes de portance. Le théorème de Bernoulli s'applique uniquement à un écoulement incompressible dont la masse volumique reste constante et à un fluide dit parfait dont on néglige les pertes de charge ainsi que les effets visqueux. La quantité de Bernoulli vérifie cette égalité : 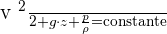 Avec :
Avec :
- v la vitesse du fluide en un point en m/s ;
- g accélération de la pesanteur en N/kg ou m/s² ;
- z l'altitude du point considéré en m ;
- p la pression en un point en Pa ou N/m² ;
- ρ la masse volumique en un point en kg/m³.
Sur une même ligne du courant, la quantité de Bernoulli se conserve et de plus, si l'écoulement est irrotationnel, alors la quantité de Bernoulli se conserve dans tout le fluide. Le théorème de Bernoulli a permis l'énonciation d'autres lois et effets :
- La loi de l'hydrostatique ;
- L'effet Magnus ;
- L'effet Venturi ;
- Le Tube de Pitot.
Rappel sur la mécanique des fluides
La mécanique des fluide est une matière de la physique qui consiste en l'étude des différents fluides qui peuvent être sous forme liquide, gazeuse ou de plasma.
Le plasma est un état de la matière, au même titre que l’état gazeux, l’état liquide ou encore l’état solide. Il se constitue en grandes parties de particules ionisées. Il a été introduit comme quatrième état de la matière en 1928 par le physicien américain Irving Langmuir. On peut le rencontrer sur Terre sous de très hautes températures. Le cœur des flammes, la foudre ou encore les étoiles sont sous l’état de plasma

La mécanique des fluides s'articule autour de deux grandes études : l'étude de l'hydrostatique et celle de la dynamique des fluides. L'hydrostatique est l’étude des fluides immobiles. Elle est également nommée statique des fluides. C'est le savant Archimède qui l'a mise au point. Elle définit l'étude de nombreux phénomènes physiques de la mécanique des fluides avec notamment les notions de pression dans un fluide, du cas particulier où ce dernier serait incompressible également. C'est grâce à cette discipline qu'on a pu mettre au point le baromètre qui permet de mesurer la pression atmosphérique. Aujourd'hui, on utilise l'hydrostatique pour de nombreuses applications :
- Mesure de la pression de l'air et de l'eau ;
- Mesure de la masse volumique ;
- Météorologie et climatologie.
La dynamique des fluides est l'étude des fluides en mouvement. Cette dernière caractérise les fluides qu'ils soient liquides ou gazeux en leur donnant diverses propriétés :
- Vitesse d'un fluide ;
- Viscosité d'un fluide ;
- Densité d'un fluide ;
- Pression d'un fluide ;
- Température d'un fluide.
Exercice d'application
Une éprouvette contenant un liquide visqueux sert de support à l’étude de la chute d’une bille d’acier. Le schéma ci-dessous, qui donne une idée du montage, n’est qu’indicatif. En particulier, il ne respecte pas d’échelle et ne peut pas servir de support pour des mesures.
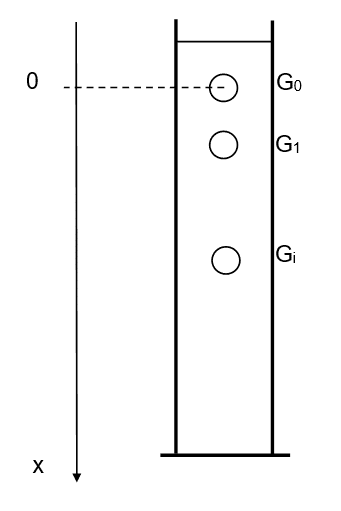
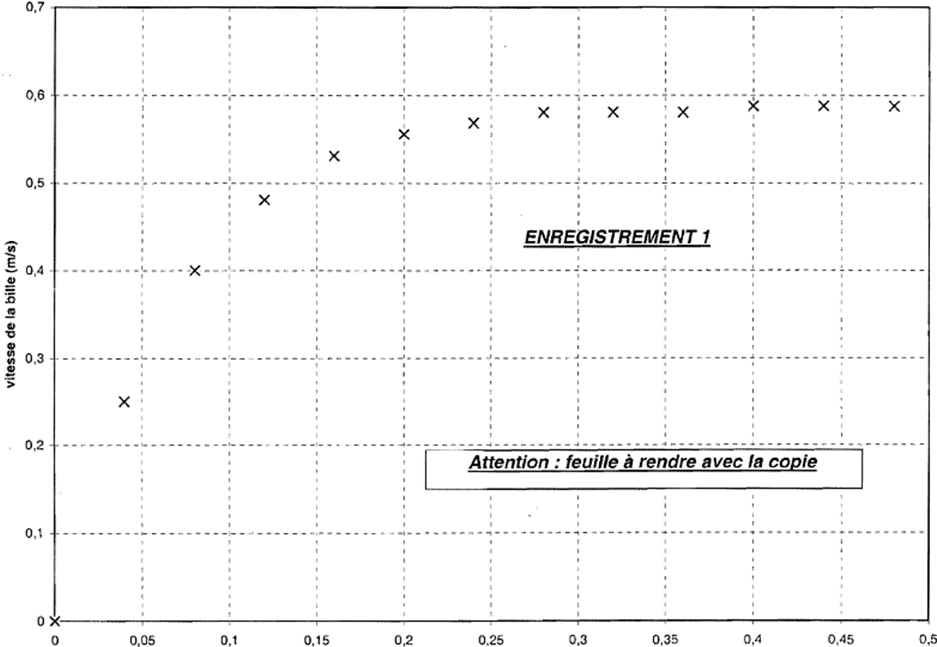
La bille, qui constitue le système étudié, est lâchée sans vitesse initiale à l’instant t = 0 (voir figure 1). Au même instant, une acquisition vidéo assurée par une webcam couplée à un ordinateur est déclenchée de manière à enregistrer 25 images par seconde. La position instantanée x du centre G de la bille est repérée par l’axe vertical orienté vers le bas , de vecteur unitaire v . A t = 0, G est en G0. Le vecteur-vitesse de G est noté. La vidéo est ensuite analysée à l’aide d’un logiciel approprié qui permet de repérer aux dates ti les positions successives xi de G lors de son mouvement descendant et de calculer approximativement la vitesse moyenne vi entre les dates t i - 1 et t i + 1. La détermination des vitesses vi aux instants ti donne l’ENREGISTREMENT 1. 3.1. Exploitation de l’enregistrement 3.1.a Expliquer comment le logiciel permet de déterminer les vitesses vi à partir des positions x i aux instants t i . 3.1.b Mettre en évidence l’existence d’une vitesse limite vl dont on donnera la valeur. 3.2. Équation du mouvement

On considère comme système la bille plongée dans le liquide et en mouvement par rapport à celui-ci. 3.2.a Faire le bilan des forces qui s’exercent sur le système. Les représenter sur un schéma. 3.2.b On note m et V la masse et le volume de la bille, r et r’ les masses volumiques respectives de l’acier qui constitue la bille et du liquide dans laquelle celle-ci est plongée. est l’accélération de la pesanteur. On suppose que la force (« résistance ») exercée par le fluide sur la bille en mouvement est de la forme , k étant une constante positive. Déterminer l’équation différentielle vérifiée par la fonction v(t). Montrer qu’elle est de la forme :  3.2.c Dans l’équation différentielle ou dans l’expression de la solution, mettre en évidence l’existence d’une vitesse limite. Calculer sa valeur et la comparer à celle trouvée en 3.1.b. Utiliser l’analyse dimensionnelle pour déterminer l’unité de m/k. Calculer numériquement ce rapport. Quelle interprétation peut-on donner de cette grandeur ? 3.3. Détermination du temps caractéristique sur l’enregistrement Par une méthode de votre choix et que vous expliciterez, déterminez sur l’enregistrement la valeur du temps t caractéristique du phénomène. Conclusion.
3.2.c Dans l’équation différentielle ou dans l’expression de la solution, mettre en évidence l’existence d’une vitesse limite. Calculer sa valeur et la comparer à celle trouvée en 3.1.b. Utiliser l’analyse dimensionnelle pour déterminer l’unité de m/k. Calculer numériquement ce rapport. Quelle interprétation peut-on donner de cette grandeur ? 3.3. Détermination du temps caractéristique sur l’enregistrement Par une méthode de votre choix et que vous expliciterez, déterminez sur l’enregistrement la valeur du temps t caractéristique du phénomène. Conclusion.























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !