Chapitres

I/Vocabulaire
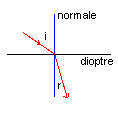
rayon incident : rayon avant réfraction
rayon réfracté : rayon dévié
La déviation s'opère juste en un point que l'on appelle
point d'incidence
- Ce point appartient à la surface qui sépare les deux milieux. Une telle surface est nommée
dioptre
- La normale est la droite perpendiculaire au dioptre au point d'incidence.
Comme pour la réflexion, nous définirons des angles :
-
- î = angle d'incidence = angle formé par le rayon incident et la normale
-
- r = angle de réfraction = angle formé par le rayon réfracté et la normale
-
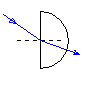
- Utilisons maintenant le disque optique avec un demi cercle en verre.
-
- Envoyons un rayon lumineux sur la surface plane (le rayon est envoyé sur le point milieu de cette face).
-
- Grâce au disque optique, nous pouvons mesurer les angles d'incidence et de réfraction.
Lorsqu'un rayon lumineux passe d'un milieu A vers un milieu B plus réfringent, il se rapproche de la normale. Si le milieu B est moins réfringent, il s'écarte de la normale.
i = 40°
r = 25°
i > r
Nous constatons donc que l'angle de réfraction est plus petit que l'angle d'incidence. Dans ce cas, on dit que le second milieu est plus réfringent que le premier milieu traversé et inversément : si r > i, alors le deuxième milieu est moins réfringent que le premier.
L'eau et le verre sont plus réfringents que l'air et l'eau est moins réfringente que le verre.
II/ Expérience de Newton (1642 – 1727)
I Expérience : on éclaire une fente avec une lumière blanche et on envoie le faisceau obtenu sur la face d'un prisme.
- Observations : la lumière est déviée par le prisme.
- De plus le faisceau qui émerge du prisme est étalé et présente les différentes couleurs de l'arc-en-ciel
- (rouge, orange, jaune, vert, bleu, indigo, violet).
- La lumière rouge est moins déviée que la lumière violette.
- Conclusion :
- Le prisme dévie et décompose la lumière blanche en lumières colorées du rouge au violet.
- C'est un phénomène de dispersion.
- L'ensemble des couleurs obtenues constitue le spectre de la lumière blanche.
- Le spectre est continu du rouge au violet.
- La lumière blanche est constituée de plusieurs couleurs ou radiations : c'est une lumière polychromatique.
- Arc en Ciel :
III/ Expérience avec la lumière émise par un Laser
I Expérience : on éclaire une fente avec un faisceau laser et on envoie le faisceau obtenu sur la face d'un prisme.
- Observation : le faisceau laser est dévié et le spectre ne comporte qu'une seule couleur, la couleur rouge initiale.
- Conclusion : la lumière produite par un laser est constituée d'une seule radiation, elle est monochromatique.
IV/ Radiation et longueur d'onde
- Une lumière monochromatique ne peut être décomposée par un prisme.
- C'est une radiation lumineuse qui est caractérisée par sa longueur d'onde λ dans le vide ou l'air. Son unité légale est le mètre (m).
- Le laser rouge utilisé au lycée est une radiation de longueur d'onde λ = 633 nm.
- C'est une lumière monochromatique.
- Remarque : une lumière complexe est un mélange de plusieurs radiations.
- Elle n'est pas caractérisée par une longueur d'onde. On lui associe une plage de longueurs d'onde.
V/ Domaine du visible
- L'œil humain n'est sensible qu'aux radiations dont les longueurs d'onde sont comprises entre 400 nm et 800 nm.
- La lumière blanche est un mélange de toutes les radiations visibles.
VI/
A) Mise en évidence
I Expérience : laser + cuve à eau.
- Observations : on constate que le faisceau lumineux change brusquement de direction quand il franchit la surface de séparation air – eau.
B) Définition
- On appelle réfraction de la lumière le changement de direction que la lumière subit à la traversée de la surface de séparation entre deux milieux transparents.
C) Première loi de Descartes
- Vocabulaire :
- SI : rayon incident et IR rayon réfracté.
- I : le point d'incidence.
- NI : normale à la surface de séparation.
- Le plan d'incidence : on appelle plan d'incidence, le plan qui contient : le rayon incident (SI) et la normale ( IR) au point d'incidence I.
- Énoncé de la première loi de Descartes : Le rayon réfracté est dans le plan d'incidence.
D) Deuxième loi de Descartes
- L'angle de réfraction i2 est généralement différent de l'angle d'incidence i1.
- Lorsque l'on trace sin i1= f (sin i2), la courbe obtenue est une droite qui passe par l'origine.
- En conséquence :
- sin i1= k . sin i2
- Ceci constitue la deuxième loi de Descartes.
E) Indice de réfraction
- Pour une radiation donnée, un milieu transparent homogène est caractérisé par un indice de réfraction n.
| n = | c |
| | |
| v |
| n est un nombre qui n'a pas d'unité et n ≥ 1 |
| n indice de réfraction |
| c vitesse de la lumière dans le vide (m / s) |
| v vitesse de la lumière dans le milieu considéré (m / s) |
- Remarque : comme c ≥ v alors n ≥ 1.
- Retour sur la relation précédente : sin i1= k . sin i2
- Question : que représente la grandeur k ?
- Le rayon lumineux passe du milieu 1 d'indice n1 au milieu 2 d'indice n2.
- Le coefficient k représente le quotient de l'indice de réfraction du milieu 2 et de l'indice de réfraction du milieu 1.
| - On écrit : | k = | n 1 | |
| | |||
| n 2 |
- La deuxième loi de Descartes s'écrit : n1. sin i1= n2 . sin i2 (1).
- Schéma.
|
|
- Lorsqu'une lumière arrive sur un prisme, elle subit deux réfractions : une sur la face d'entrée et une sur la face de sortie.
- Deuxième loi de la réfraction : n1. sin i1= n2 . sin i2 (1).
- Le trajet d'une radiation dépend de l'indice du prisme car l'angle d'incidence est le même pour les différentes radiations qui constituent la lumière blanche.
- Le trajet d'une lumière dans le prisme dépend de sa couleur.
- Or ce trajet dépend de l'indice du prisme.
- L'indice du prisme dépend de la fréquence ou de la longueur d'onde dans le vide de la radiation.
- L'indice de réfraction d'un milieu transparent dépend de la longueur d'onde (dans le vide) de la radiation qui s'y propage.
- Exemple :
| Pour le verre ordinaire : | n rouge = 1,510 | nbleu = 1,520 |
| Pour l'eau : | n rouge = 1,330 | n bleu = 1,336 |
- Avec cabri géomètre : figure prisme.
|
|























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Ton cours est tres bien, les explications sont claires etc. mais je ne trouve rien concernant la relation liant la frequence, la longueur d’onde et la vitesse dans le vide. Tu ne parles pas de lambda etc. alors que tu montres un arc-en-ciel.
En tout cas merci pour ta publication, les cours sont rarement aussi clairs. Bravo :-)