Chapitres

Mesures directes de longueurs
Afin de mesurer des longueurs, et ce notamment en physique et en chimie, on utilise des unités plus petites que le millimètre. On retrouve donc le nanomètre qui mesure 0,000001 millimètres et le micron qui mesure 0,001 millimètre et 1000 nanomètres. Enfin, il existe aussi des autres unités de mesure telles que :
- Le pouce : unité anglaise datant du Moyen-Âge, 1 mètre vaut 39,37008 pouces ;
- Le pied : unité de longueur qui correspond à la longueur d'un pied humain. Un pied mesure 12 pouces et 0,3048 mètres ;
- Le mile : unité de mesure en regroupant plusieurs comme le mile marin qui mesure 1,852 kilomètres et le mile international, une unité anglaise qui représente 1,609 kilomètre.
Les unités de longueurs
Des préfixes ont été ajoutées aux unités de base du Système International afin de pouvoir plus facilement manier de grands nombres. La plupart du temps, ces préfixes sont utilisés en lieu et place des ordres de grandeur. On parlera d’un kilo pour exprimer une grandeur d’ordre 103 ou d’un méga pour exprimer une grandeur d’ordre 106. Nous comptons 20 préfixes aux unités de grandeur. Ces derniers sont apparus pour la plupart au cours du 20e siècle mais certains existent depuis le 18e siècle ! C’est souvent dans le domaine de l’informatique que vous entende parler de ces ordres de grandeur. En effet, si l’on parle d’ 1 examètre, on préférera utiliser l’appellation de 105,7 années lumières. Cependant, si vous utilisez des clés USB ou des disques durs, vous aurez souvent entendu parler que ces derniers ont des capacités qui se mesurent en gigabits ou encore térabits.
Yocto
Le yocto représente 10-24 fois l'unité de base, soit un quatrillionième. Il est représenté par un petit y.
Zepto
Le zepto, de symbole petit z est l'avant dernière grandeur la plus petite du Système International. Il représente un millième de milliardième de milliardième de l'unité de base, soit 10-21.
Atto
L'atto est un milliardième de milliardième. Il représente 10-18 fois l'unité de base du Système International. Il se note avec un petit a comme symbole.
Femto
De symbole petit f, le femto est le représentant de 10-15 fois l'unité du Système International. C'est donc un millionième de milliardième. Son origine est le mot femten, du danois qui signifie quinze.
Pico
Le pico représente 10-12 unités. C'est donc un billionième d'unité du Système International. Cette appellation provient de l'italien piccolo qui signifie petit. Son symbole est le petit p.
Nano
Cette unité, crée en 1960, tire son origine du mot nain en grec, nanos. Elle représente 10-9 unités du Système International, soit un milliardième d'unité. Il est représenté par un petit n en guise de symbole.
Micro
Le préfixe micro représente un millionième d'unité du Système International, soit 10-6. Il est représenté par la lettre µ, mu, en grec. Son nom provient du mot microscopique, qui signifie un élément tellement petit qu'on ne peut le voir qu'au microscope.
Milli
Le préfixe milli représente 10-3 unités du Système International, soit un millième. Il est représenté par un petit m.
Centi
Le centi représente un centième d'unité, soit 10-2. C'est donc un centième qui se note avec un petit c.
Déci
Le déci, de symbole petit d, est l'unité qui représente un dixième de l'unité de base du Système International. C'est donc 10-1 fois cette unité.
L'unité de base
Entre le déci est le déca se trouve l'unité de base du Système International. Cette dernière est égale aux nombres compris entre 0 et 10. Elle se note en ordre de grandeur 100, ce qui est égal à 1.
Déca
Le préfixe déca, de symbole da est à ne pas confondre avec le déci. Il représente bien 101, soit une dizaine de l'unité de base du Système International et non pas 10-1.

Hecto
Le préfixe hecto sert à désigner une unité de l'ordre de grandeur 102. Il représente donc une centaine de l'unité de base du Système International. Cette unité est peu couramment utilisée au quotidien. C'est dans le domaine de l'agroalimentaire qu'elle prend tout son sens. Son symbole est un petit h.
Kilo
Le kilo est l'unité qui représente le millier. D'ordre de grandeur 102, c'est l'une des plus utilisée dans notre vie quotidienne. Elle se note avec le symbole k et représente un millier d'unités de base.
Méga
L'unité définie par le méga se note avec un grand M et représente un million d'unités de base du Système International, c'est donc 106.
Giga
Le giga est un préfixe utilisé fréquemment en informatique. Il représente 109, c'est à dire un milliard d'unités du Système international. Son symbole est un grand G.
Péta
Le suffixe péta est là pour représenter un billiard, ou million de milliards de l'unité de base. C'est donc un nombre d'ordre de grandeur 1015. Il se note avec un grand P en guise de symbole.
Exa
L'exa représente un trillion de l'unité de base du Système International, soit un milliard de milliards. Son ordre de grandeur est 1018. Il est exprimé par le symbole d'une grande lettre E.
Zetta
Le zetta, est l'expression de 1021 unités de base du Système International. C'est donc un billion de billiards, aussi appelé trilliard. C'est une grandeur extrêmement grande et elle est l'avant dernière plus grande qui existe. Elle se note avec un grand Z.
Yotta
Le yotta est l'unité la plus grande qui existe au monde, elle représente un quadrillion, ou un billiard de milliars, soit 1024 unités de base. Cela signifie qu'un yotta est égal à un 1 suivi de vingt-quatre 0 ! Il se note avec un grand Y.
Appareils de mesures
Pour effectuer des mesures de longueurs, on utilise différents appareils. Nous allons ici vous les présenter.
Le vernier
Egalement connu sous le nom de palmier ou pied à coulisse, le vernier est un appareil de mesure avec une réglette graduée sur un pied à coulisse qui permet d'effectuer des mesures de précision.
Il tient son nom de son inventeur : Pierre Vernier. Il s'agit d'un ingénieur militaire et mathématicien français ayant vécu entre 1580 et 1638. Il a longuement travaillé sur les mesures d'angles et les instruments de mesure, dont le vernier est sa plus célèbre.
Son fonctionnement est simple : un règle graduée sur laquelle coulisse un vernier. L'écartement entre le vernier et le bout de la règle donne alors la mesure.

La chevillère
Il s'agit du nom scientifique du mètre à ruban. Il se décrit comme un ruban souple gradué à intervalles réguliers.
Son utilisation principale est celle de la couture. En effet, la souplesse du ruban permet de mesurer facilement les longueurs des habits. On les retrouve aussi sur les chantiers du bâtiment pour mesurer des grandes longueurs.
Leur longueur est souvent un multiple de 10. En couture, la chevillère mesurera souvent jusqu'à 100 cm et pour les chantiers, elle mesurera des fois plusieurs centaines de mètres.
Le curvimètre
Le curvimètre est un petit instrument de mesure que l'on utilise pour effectuer des mesures sur un carte.
Composé d'une petite roue et d'un cadran avec une aiguille, le curvimètre permet de mesurer la longueur d'un trajet et ce même s'il n'est pas rectiligne.
Parfois, le cadran dispose de plusieurs échelles afin de mesurer les distances selon les échelles les plus utilisées des cartes.
Le kutsch
Egalement connu sous le nom de règle à échelles ou règle à échelles multiples, le kutsch se présente sous la forme d'une règle à trois faces dont chaque face dispose d'une échelle différente.
Habituellement, ces règles mesurent 30 cm et proposent ces échelles :
- 1/500, 1/1000, 1/1250, 1/1500, 1/2000,1/2500 ;
- 1/100, 1/200, 1/250, 1/300, 1/400, 1/500 ;
- 1/20, 1/25, 1/50, 1/75, 1/100, 1/125.
On utilise beaucoup le kutsch en architecture pour réaliser des plans à l'échelle.
Le mètre pliant
Le mètre pliant est un mètre constitué de plusieurs parties qui se déplie à la manière d'un accordéon. De précision limitée, il est souvent utilisé dans les métiers du bâtiments pour effectuer des mesures rapides de petites longueurs.
Ses différents segments mesurent habituellement 20 centimètres et se succèdent sur 1 mètre ou 2 mètres.
Le mètre ruban
Le mètre ruban est le mètre standard que l'on rencontre le plus couramment. Constitué d'un ruban enroulable, il permet d'effectuer les mesures de base du quotidien.

Régulièrement rétractable, il tient dans une poche ou une caisse à outil.
On en trouve allant de 1 mètre à 10 mètres, en plastique ou en métal.
Exemples de mesures
| Élément | Appareil de mesure | Mesure |
|---|---|---|
| Diamètre d'un cheveu | Vernier | 0,02 mm |
| Longueur d'un couloir | Mètre standard | 43,9 m |
| Épaisseur d'un pied de table | Pied à coulisse | 35 mm |
| Longueur d'une route sur une carte routière | Curvimètre | 120 km |
Critiques des résultats
Au niveau du Cheveu : Attention à bien annoncer la bonne unité
dcheveu ≈
0,004 mm.
Au niveau de l'épaisseur du pied de table : Pas de problème de mesure, ni d'unité.
Au niveau de la longueur du couloir : Le Couloir ne semble pas faire la même longueur pour tout le Monde ? En effet, si l'on compare les résultats, il semble impossible de donner une précision au centimètre prés, ni à 10 cm. Par contre, en annonçant tout les résultats au mètre près, tout le monde semble satisfait pour donner :
Lcouloir
≈ 44 m.
Interprétation
On doit donc adapter la précision d'un résultat à la précision d'un instrument de mesure, et de tenir compte de tout ce qui peut entraîner des incertitudes. Quand on annonce dcheveu ≈ 0,04 mm, cela signifie que la valeur exact est comprise entre 0,035 mm et 0,045 mm.
0,035 < Valeur exacte < 0,045
De même, quand on annonce que la largeur du couloir est d'environ 44 mètres, cela signifie que la valeur exacte est comprise entre 43,5 m et 44,5 m.
43,5 < Valeur exacte < 44,5
Au niveau du cheveu : En annonçant 0,04 mm, je suis peut être ( au pire des cas ) à 0,005 mm de la valeur exacte.
Étude rigoureuse
Est-ce que 0,005 mm, présente un taux important par rapport au diamètre du cheveu ?
Pour le savoir, j'effectue le calcul suivant, et je l'interprète le résultat en pourcentage.
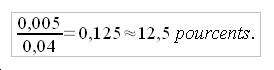
Cela signifie, que lorsque j'annonce 0,04 mm, je suis peut être à 12,5% de la valeur exacte. ( Ce qui n'est pas très précis).
Au niveau du couloir : En annonçant 44 mètres, je suis peut être ( au pire des cas ) à 0,5 m de la valeur exacte.
Mesure indirecte de distance
Définition
Une mesure indirecte de longueur est une mesure que l'on effectue pas avec un instrument de mesure mais par le biais d'un calcul mathématique ou géométrique.
En effet, il arrive souvent qu'il soit impossible d'effectuer des mesures car ces dernières sont trop grandes. C'est le cas par exemple de la distance entre deux planètes, de la hauteur d'une montagne ou encore de la taille d'un gratte-ciel. Nous devons alors avoir recours à des calculs. Si par les passé ces derniers s'effectuaient à la main, il est maintenant possible d'utiliser des instruments de plus en plus précis qui effectuent ces calculs à notre place.
Des instruments de mesure indirectes
Le télémètre laser
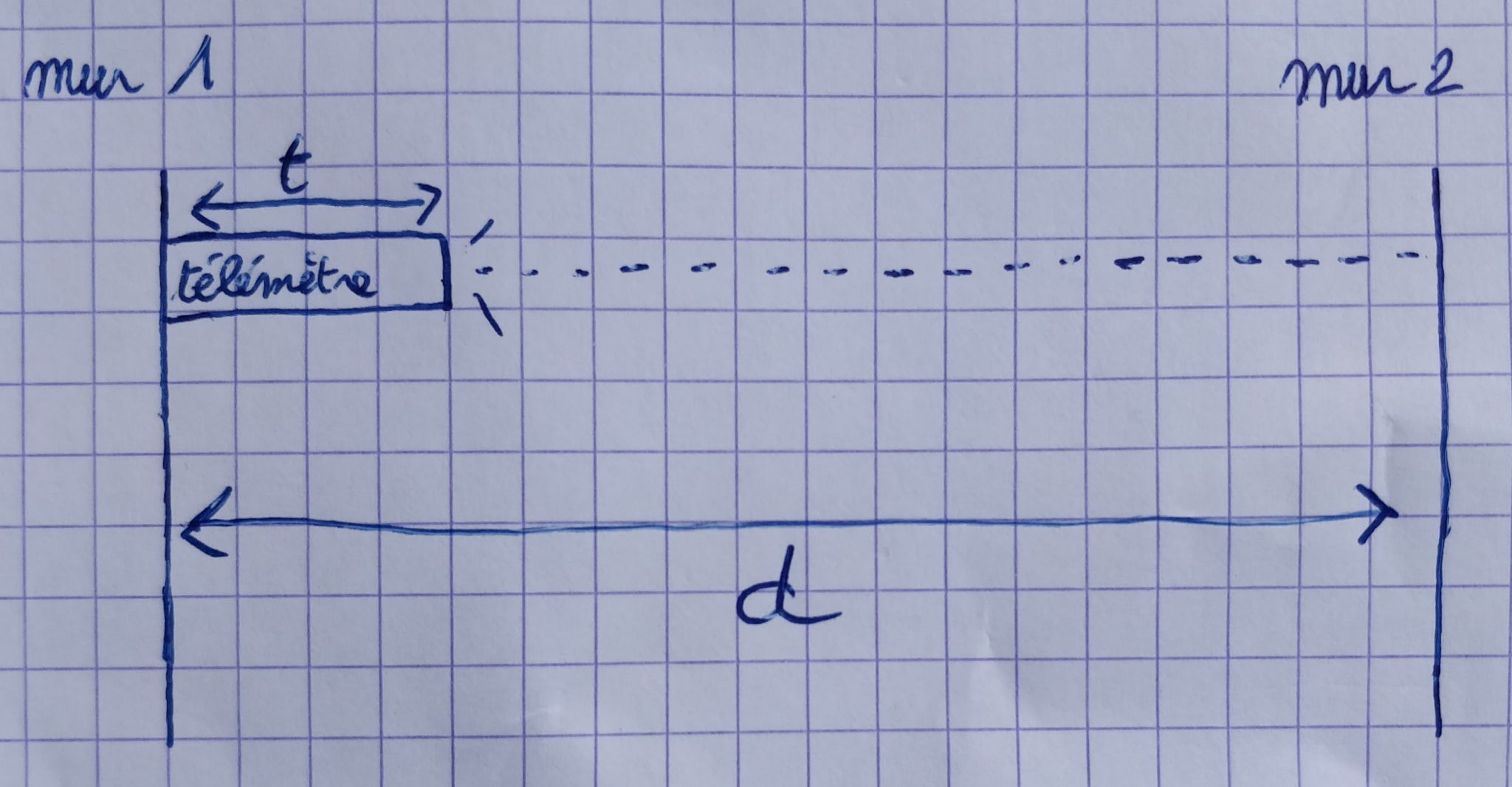
Le télémètre laser est un appareil qui permet de mesurer des distances, utilisé dans le bâtiment, il permet aux ouvrier de mesurer par exemple de mesurer l'espacement entre deux murs de façon rapide et précise.
Son fonctionnement est simple, il envoie un signal laser à la cible qui le réfléchit. En calculant le déphasage, on peut alors connaître la distance entre les deux objets.
Le radar
Un peu sur le même principe que le télémètre laser, le radar envoie un signal sonore vers une cible qui la lui renvoie. En calculant le temps entre le départ de l'onde et son retour, on peut alors connaître sa distance. La même opération effectuée de nouveau après un temps donné donne alors une deuxième distance qui permet de calculer la vitesse par effet Doppler.

La trigonométrie
On peut avoir recours à des théorèmes de trigonométrie pour calculer la hauteur d'une montagne ou d'un gratte-ciel par exemple. On utilisera alors le théorème de Pythagore ou encore le théorème de Thalès.
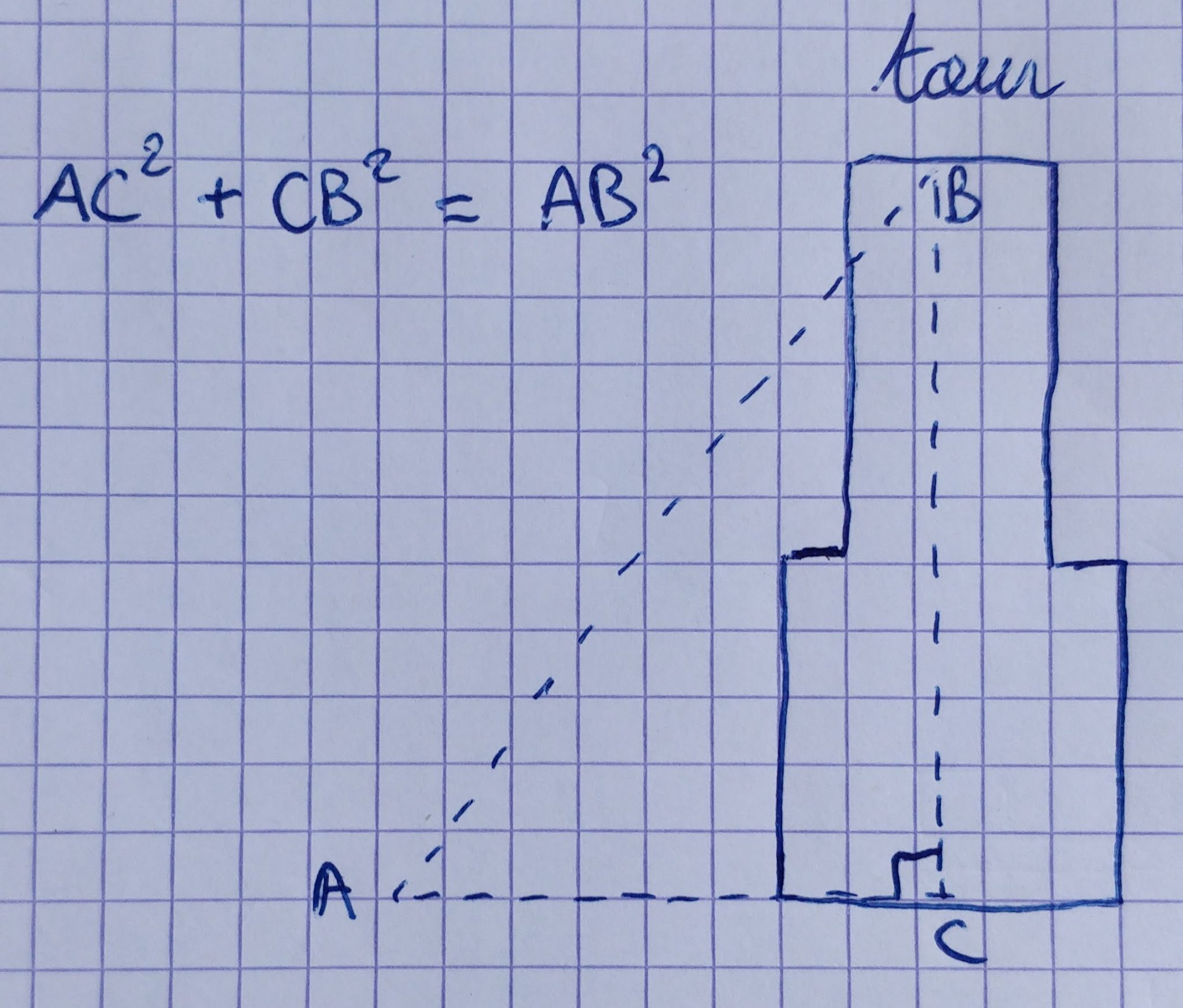
Exemple concret
Un personnage se situe au niveau d'une rivière, en regardant de l'autre côté de la rive, il aperçoit un arbre. Il souhaiterait connaître sa distance par rapport à cette arbre. Cependant, cet individu ne dispose que de petits cailloux et de son cerveau. Il sait également, que son pas est environ égale à 1 mètre.
Comment peut-il s'y prendre ?
Il est préférable et fortement recommandé, de réaliser un schéma.
Évitez les perspectives car les angles et les distances sont déformés.
Choisissez une vue qui permet de bien voir ce qu'on cherche et ce que l'on connaît. ( Ici, vue de dessus ).
Ne pas prendre des cas particuliers si ce n'est pas dit ( Ne pas inventer de données ).
Nommer chaque chose par une lettre.
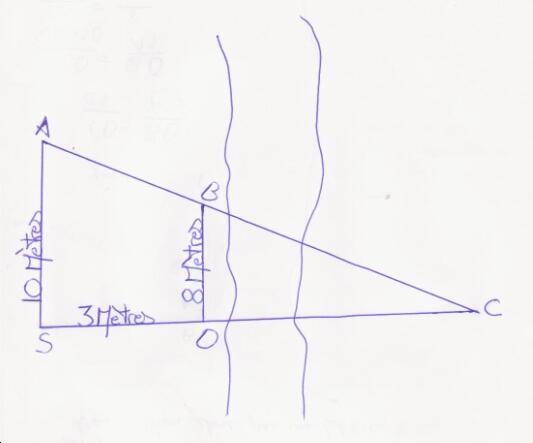
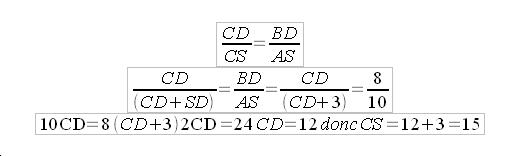
L'individu se situe à 15 mètres de l'arbre.






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !