Chapitres

Introduction
Une orbite est la trajectoire courbe que forme une planète lors de ses mouvements dans l'espace. Cette trajectoire est causée par la gravitation et l'inertie de la planète autour d'un autre astre.
Dans cet article nous allons voir comment fonctionnent ces orbites, ce à quoi elles sont dues et comment elles s'expriment dans un cas particulier : notre Système Solaire.
La découverte des orbites
Depuis longtemps les hommes proposaient des modèles pour expliquer que les planètes en mouvement étaient visibles de manière périodique dans le ciel.
Cependant, les premiers modèles, géocentriques, sont encore bien loin de la réalité.
Le modèle géocentrique, ou géocentrisme, est un modèle physique planétaire qui place la Terre au centre de l’Univers. Datant de l’Antiquité, ce sont les savants Aristote et Ptolémée qui l’ont défendu. Ce n’est qu’à la renaissance qu’il sera délaissé au profit du système héliocentrique, mettant le Soleil au centre du Système Solaire et la Terre en orbite autour de cet astre.
Il faudra attendre Galilée et Copernic pour entendre les scientifiques commencer à accepter l'idée d'un système héliocentrique.
En 1600 sont évoquées trois lois par Kepler, les fameuses Lois de Kepler qui décrivent les trajectoires prises par les planètes du Système Solaire :
- Les planètes décrivent des ellipses dont le Soleil occupe l'un des foyers ;
- Le rayon vecteur reliant le centre de la planète au foyer décrit des aires égales en des temps égaux ;
- Les cubes des demi-grand axes des orbites sont proportionnels au carré des périodes de révolution.
On parlera alors d'orbite képlérienne.
Orbite keplérienne
Une orbite keplérienne est une orbite dont le corps est assimilable à un point. Cette assimilation peut se faire simplement si la distribution des masses est une symétrie sphérique.
Les orbites keplériennes sont des orbites coniques dont l'un des foyers est le centre de masse du corps en orbite. On le considère alors comme origine du référentiel.
Galilée
Ce savant réalisera pendant sa vie de nombreux outils tels que la lunette astronomique en perfectionnant la lunette d'approche découverte par des Hollandais afin de procéder à des observations rapides mais aussi précoces. Cette lunette aura par ailleurs bouleversé de nombreux fondements de l'astronomie de l'époque. Galilée aura également été grand défenseur de l'approche modélisatrice copernicienne de l'Univers. Il lui proposera d'ailleurs d'adopter l'héliocentrisme et les mouvements satellitaires. A cause de ses prises de position, il s'attira les foudres et les critiques de nombreux philosophes, partisans d'Aristote, qui proposaient un géocentrisme stable, une classification des corps et des êtres, un ordre immuable des éléments mais également une évolution réglée des substances. Malgré les mises en garde de ses différents protecteurs religieux, Galilée manquera de prudence au sujet de sa prise de position du mouvement terrestre, celui-ci ne possédant pas de preuves de ce qu'il avançait.

En ce qui concerne les mathématiques, Galilée n'a aucunement contribué à la progression de l'algèbre mais il aura beaucoup travaillé sur les suites mais également les courbes géométriques et la prise en compte de l'infiniment petits. D'ailleurs, Galilée décrira les mathématiques comme étant "un langage décrivant la nature".
Galilée aura également permis de nombreuses avancées concernant la mécanique, notamment la cinétique et la dynamique, grâce aux bases qu'il aura posé avec l'aide de ses nombreuses expériences sur l'équilibre mais aussi le mouvement des corps solides, en particulier sur la chute, la translation rectiligne, l'inertie mais également la généralisation des mesures dont le temps par l'isochronisme du pendule et la résistance des matériaux. Il sera même considéré comme fondateur de la physique -première des sciences exactes modernes- à partir de 1680.
Vous cherchez un professeur de sciences physiques ?
Observer une planète sur son orbite : la lunette de Galilée
La lunette astronomique plus en détail
La lunette astronomique, également appelée lunette de Kepler, est un instrument optique composé de lentilles lui permettant ainsi d'augmenter la luminosité mais également la taille apparente des objets célestes lors de l'observation de ceux-ci. Lorsque la lunette de Kepler est équipée d'un redresseur d'image, elle se comportera alors de façon similaire à la lunette d'approche, également appelé longue-vue.
Cet instrument a été développé dès la fin du XVIe siècle mais il faudra attendre 1609 pour que la lunette astronomique soit utilisée afin de réaliser des observations systématiques du ciel.
Historique de cet outil
Personne ne sait dire précisément qui a inventé la lunette astronomique. En effet, dans certains écrits de Leonard Digges, on peut comprendre que celui-ci avait conçu un prototype dès les années 1550 même si les premiers exemplaires explicitement décrits sembleraient venir d'Italie ou du Nord de l'Europe. En effet, Giambattista della Porta mentionna la lunette de Kepler dans son ouvrage La Magie naturelle en 1859. De nombreuses personnes cherchèrent alors a obtenir le brevet de cette lunette comme Hans Lippershey qui sera le premier a réaliser une démonstration concrète de la lunette d'approche avec un grossissement trois. En Septembre 1608, il semblerait que Zacharias Janssen en aurait commercialisé lors de la foire d'automne de Francfort. Jacques Metius, soutenu par Descartes se lança également dans la course au brevet.
D'ailleurs, le célèbre Descartes parlera de cette invention dans son ouvrage la Dioptrique :
« Mais, à la honte de nos sciences, cette invention, si utile et si admirable, n'a premièrement été trouvée que par l'expérience et la fortune. Il y a environ trente ans, qu'un nommé Jacques Metius, de la ville d'Alkmaar en Hollande, homme qui n'avait jamais étudié, bien qu'il eût un père et un frère qui ont fait profession des mathématiques, mais qui prenait particulièrement plaisir à faire des miroirs et verres brûlants, en composant même l'hiver avec de la glace, ainsi que l'expérience a montré qu'on en peut faire, ayant à cette occasion plusieurs verres de diverses formes, s'avisa par bonheur de regarder au travers de deux, dont l'un était un peu plus épais au milieu qu'aux extrémités, et l'autre au contraire beaucoup plus épais aux extrémités qu'au milieu, et il les appliqua si heureusement aux deux bouts d'un tuyau, que la première des lunettes dont nous parlons, en fut composée. »
Une fois que la lunette d'approche fut connue et commercialisé, plusieurs personnalités dès 1609 décidèrent de s'en servir afin d'observer les astres comme Thomas Harriot et Christoph Scheiner. Il faudra tout de même attendre Galilée qui, en Août 1609, établira réellement l'utilisation de la lunette d'approche pour l'observation d'astres. De plus, avec son regard curieux et neuf sur le sujet, il réalisa l’existence de différent phénomènes qu'il observera et étudiera. Au final, il décida de mettre au point ses propres lunettes d'observation avec des grossissement par six, vingt puis finalement trente.
Comme peut indiquer le nom de cet instrument, les lunettes de Galilée correspondent à deux lunettes astronomiques qui ont été conçues par Galilée. Ces deux lunettes étant destinées à l'observation du ciel et des astres.
Il n'existe que deux originaux qui sont actuellement conservés au Musée de Galilée à Florence. On les nommera plus tard télescope suite à la proposition du prince Federico Cesi, aussi connu comme étant le fondateur de l'Académie des Lyncéens. Il a décidé de ce nom en combinant le préfixe tele, signifiant loin, et le verbe skopeo, signifiant voir, en grec ancien. Ainsi, les lunettes de Galilée correspondent à des télescopes qui sont réfracteurs. Notons qu'en Français, le nom télescope est réservé aux télescopes réflecteurs.
En plus de ces lunettes, Galilée permettra également la conception de différents accessoire pour l'utilisation du télescope comme un micromètre permettant de mesurer la distance entre Jupiter et ses satellites, ou encore un hélioscope qui, quant à lui, permet d'observer les tâches solaires sans endommager les yeux de l'observateur.
Comment trouver un professeur physique chimie ?
Composition d'une lunette astronomique
Une lunette astronomique est composé d'un tube fermé où sont disposés d'une part et d'autre de celui-ci un objectif et un oculaire.
Le tube peut être fixe ou télescopique, notamment dans le cas des longues-vues utilisées par les marins. L'oculaire est situé, comme son nom peut laisser entendre, du côté de l’œil de l'observateur. Il est de petite taille. L'objectif, quant à lui, se situe de l'autre côté du tube et est généralement de plus grande taille que l'oculaire.
La lunette de Galilée
Comme peut indiquer le nom de cet instrument, les lunettes de Galilée correspondent à deux lunettes astronomiques qui ont été conçues par Galilée. Ces deux lunettes étant destinées à l'observation du ciel et des astres.
Il n'existe que deux originaux qui sont actuellement conservés au Musée de Galilée à Florence. On les nommera plus tard téléscope suite à la proposition du prince Federico Cesi, aussi connu comme étant le fondateur de l'Académie des Lyncéens. Il a décidé de ce nom en combinant le préfixe tele, signifiant loin, et le verbe skopeo, signifiant voir, en grec ancien. Ainsi, les lunettes de Galilée correspondent à des télescopes qui réfracteurs. Notons qu'en Français, le nom télescope est réservé aux télescopes réflecteurs.
En plus de ces lunettes, Galilée permettra également la conception de différents accessoire pour l'utilisation du télescope comme un micromètre permettant de mesurer la distance entre Jupiter et ses satellites, ou encore un hélioscope qui, quant à lui, permet d'observer les tâches solaires sans endommager les yeux de l'observateur.
L'Académie des Lyncéens
Egalement appelée Académie des Lyncées ou Académie des Lynx, cette académie est considérée comme étant la plus ancienne académie scientifique d'Europe. Elle sera fondée en 1603 par un pacte entre le prince Federico Cesi et deux de ses amis. Cette académie adoptera la référence à la vue du lynx, connue pour être perçante, afin de symboliser la puissance de la vue de la sciences mais également la découverte de le fabuleux pouvoir de résolution du microscope, un outil inventé au XVIIe siècle qui permettra de nombreuses découvertes sur la nature de l'Homme.
La création de cette académie représentera un moment puissant de la révolution scientifique de la Renaissance puisqu'elle permettra la fondation d'une nouvelle tradition, la tradition des académies, des sociétés savantes mais également celle d'autres réseaux de correspondants initiés.
Aujourd'hui, on considère que les héritiers de cette académie sont :
- l'Accademia nazionale dei Lincei, italienne ;
- et l'Académie pontificale des sciences ou Pontificia Academia Scientiarum, du Vatican.

Première lunette de Galilée
Cette lunette correspond à un système afocal composé d'un tube principal ainsi que deux sections, considérées comme mineures, dans lesquelles on peut trouver l'objectif mais aussi l'oculaire. Quant à lui, le tube principal est composé de deux tubes semi-circulaires recouverts de papiers et tenus ensemble avec l'aide d'un fil de cuivre.
L'objectif, biconvexe, mesure 51 millimètres de diamètres. Notons que les rayons de courbure des surfaces ne sont pas pareils. La distance focale est de 1 330 millimètres et son épaisseur au centre es de 2,5 millimètres.
L'occulaire, plan-concave, mesure 26 millimètres de diamètre où le côté concave présente un rayon de courbure en direction de l'oeil de 48,5 millimètres. Son épaisseur au centre est de 3 millimètres pour une distance focale de -94 millimètres -notons que cette distance focale est négative puisque la lentille est divergente-.
Ainsi, cette lunette permet à l'observateur de visualiser des objets grossis 14 fois avec un champ visuel de 15'.
Deuxième lunette de Galilée
La deuxième lunette de Galilée, quant à elle, est composé d'un tube principal où on peut trouver à l'une de ses extrémité deux sections distinctes qui y sont insérées afin de porter un objectif et un oculaire.
Le tube est composé de lamelles de bois jointes et recouvertes de cuir rouge, aujourd'hui devenu marron à cause du temps, décoré avec des frises en or.
L'objectif, plan-convexe, présente son côté convexe vers l'extérieur mesure 37 millimètres de diamètre pour une ouverture de 15 millimètres et une distance focale de 980 millimètres. Son épaisseur au centre est de 2 millimètres.
Malheureusement, l'oculaire d'origine a été perdu mais remplacé dès le XIXe siècle par une oculaire biconcave de 22 millimètres de diamètre. Avec une épaisseur au centre de 1,8 millimètre, cet oculaire présente une distance focale de -47,5 millimètres -encore une lentille divergente, reconnaissable à la distance focale négative.
L'instrument ainsi formé permet d'agrandir 21 fois l'objet observé avec un champ visuel de 15'.
Enregistré dans l'inventaire de 1704 de la Galerie des Offices, l'oculaire, décrit comme incliné, était toujours présent bien que détaché du tube. Il sera considéré comme perdu dès le XVIIIe siècle.
La Galerie des Offices correspond à un palais florentin où y est abrité un patrimoine artistique extrêmement connu à travers le monde. Ouvert depuis 1765, le musée des Offices permet aux visiteurs d'observer sur 8 000 m² une superbe collection de peintures italiennes et autres œuvres de célèbres maîtres européens comme Albrecht Dürer et Francisco de Goya.
Les paramètres d'une orbite
Définir une orbite nécessite plusieurs paramètres. Tout d'abord, il faut définir deux plans : le plan de l'orbite et le plan de référence. Sur ces deux plans s'ajoutent d'autres caractéristiques :
- Le demi-grand axe ;
- L'excentricité ;
- L'inclinaison ;
- La longitude du nœud ascendant ;
- L'argument du périastre.
Le demi-grand axe
Cette caractéristique représente la moitié de la distance qui sépare le péricentre de l'apocentre (= le plus grand diamètre de l'ellipse). Il permet alors de définir la taille absolue de l'orbite bien que cela n'ait de sens que dans le cas d'une trajectoire elliptique ou circulaire.
L'excentricité
Cette caractéristique représente le décalage des foyers par rapport au centre de l'ellipse via le rapport de la distance centre-foyer au demi-grand-axe.
L'inclinaison
Elle correspond à l'angle de nutation. C'est à dire l'angle que fait le plan orbital avec le plan de référence.
La longitude du nœud ascendant
Il correspond à l'angle créé entre la direction du point vernal et la ligne des nœuds dans le plan de l'écliptique.
L'argument du périastre
Cette caractéristique correspond à l'angle de rotation propre et donc l'angle formé par la ligne des nœuds et la direction du périastre dans le plan orbital.
Exercices d'application
La mise en orbite d'un satellite artificiel

D'après Encyclopedia Universalis (1998) :
(Certains renseignements et données sont nécessaires à la résolution du sujet).
Le premier lanceur Ariane est une fusée à trois étages dont la hauteur totale est de 47,4 m et qui pèse, avec sa charge utile (satellite), 208 tonnes au décollage.
Le premier étage qui fonctionne pendant 145 secondes est équipé de 4 moteurs Viking V alimentés par du peroxyde d'azote N2O4 (masse de peroxyde emportée : 147,5 tonnes).
L'intensité de la force de poussée totale de ces 4 réacteurs est constante pendant leur fonctionnement: elle vaut F = 2445 kN.
Ce lanceur peut mettre en orbite circulaire basse de 200 km d'altitude un satellite de 4850 kg; il peut également placer sur une orbite géostationnaire un satellite de 965 kg; il peut aussi être utilisé pour placer en orbite héliosynchrone des satellites très utiles pour des applications météorologiques.
1. L'ascension de la fusée Ariane
Le champ de pesanteur g est supposé uniforme : son intensité est g0 = 9,8 m.s –2.
On choisit un axe Oz vertical dirigé vers le haut.
On étudie le mouvement de la fusée dans le référentiel terrestre qu'on suppose galiléen.
a) Représenter clairement, sur un schéma, en les nommant, les deux forces qui agissent sur la fusée Ariane lorsqu'elle s'élève verticalement. On néglige les frottements et la poussée d'Archimède dans l'air.
b) A un instant quelconque, la masse de la fusée est m.
Déterminer en fonction de m et des intensités des 2 forces précédentes la valeur de l’accélération a.
c) On considère d'abord la situation au décollage. La masse de la fusée vaut alors m1. Calculer la valeur numérique de l’accélération a1 à cet instant.
On envisage la situation qui est celle immédiatement avant que tout le peroxyde d'azote ne
soit consommé. La masse de la fusée vaut alors m2. Calculer la valeur numérique de m2 puis celle de l'accélération a2 à cet instant.
Le mouvement d'ascension de la fusée est-il uniformément accéléré ?
d) La vitesse d'éjection des gaz issus de la combustion du peroxyde d'azote est donnée par la relation :
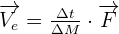
où  est l’inverse de la variation de masse de la fusée par unité de temps et caractérise la consommation des moteurs.
est l’inverse de la variation de masse de la fusée par unité de temps et caractérise la consommation des moteurs.
Vérifier l'unité de Ve par analyse dimensionnelle. Calculer la valeur numérique de Ve.
A l'aide d'une loi connue qu'on énoncera, expliquer pourquoi l'éjection des gaz propulse la fusée vers le haut.
2) Étude du satellite artificiel situé à basse altitude (h = 200 km)
On s'intéresse au mouvement d'un satellite artificiel S, de masse ms, en orbite circulaire (rayon r)
autour de la Terre de masse MT, de rayon RT et de centre O.
On suppose que la Terre est une sphère et qu'elle présente une répartition de masse à symétrie
sphérique et que le satellite peut être assimilé à un point.
a) Préciser les caractéristiques du vecteur accélération d'un point animé d'un mouvement circulaire uniforme de rayon r et de vitesse v.
b) Enoncer la loi de la gravitation universelle. On appelle G la constante de gravitation universelle.
Faire un schéma sur lequel les vecteurs-forces sont représentés.
c) Le satellite S est à l'altitude h : on a donc r = R + h
On appelle la force qu'exerce la Terre sur le satellite. Cette force dépend de la position du satellite et on pose = ms.(h) . On note g(h) l'intensité de la pesanteur (h) à l'endroit où se trouve le satellite: =g(h).
Exprimer g(h) en fonction de MT, RT, h et G puis g(h) en fonction de RT, h et g0 = g(0).
d) Appliquer la deuxième loi de NEWTON au satellite en orbite circulaire
En déduire l'expression de la vitesse vs du satellite en fonction de g0 , RT et h puis celle de sa période de révolution Ts.
e) Application numérique
Calculer vs et Ts sachant que g0 = 9,8 m.s -2 ; h = 200 km et RT = 6400 km.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !