L'ensemble de Julia est une merveille mathématique, offrant des formes infiniment complexes qui émergent à partir d'une simple équation. Comme son célèbre cousin, l'ensemble de Mandelbrot, il présente une beauté fractale fascinante, où chaque zoom révèle de nouveaux motifs auto-similaires.
En explorant les propriétés de cet ensemble, on découvre une richesse de détails mathématiques qui relie la théorie des systèmes dynamiques aux applications concrètes, tout en inspirant l'art et la science.
Pour tout savoir du monde des fractales et leur découverte au début du XXème siècle, notamment à travers les travaux de Gaston Julia, lisez les détails proposés dans notre article !
La découverte de l'infini grâce à Gaston Julia
Vous vous êtes déjà demandé si l'infini existait ?
C'est bien ce que des chercheurs et scientifiques se sont demandé au cours de leur carrière, comme Gaston Julia. Mathématicien français né en 1893 en Algérie, il est affecté par son engagement durant la Première guerre mondiale, et devient une gueule cassée. Gaston Julia a d'ailleurs mené une carrière académique prestigieuse en tant que professeur de mathématiques :
- Après un doctorat en mathématiques appliquées, il lance des recherches sur les dynamiques holomorphes, qui consiste à décrire la complémentarité des ensembles selon leur comportement
- Après avoir obtenu son doctorat, il a enseigné à l'École Normale Supérieure, où il a formé plusieurs générations de mathématiciens
Avant ses travaux, les bases théoriques des ensembles fractals et des systèmes dynamiques se dessinaient déjà au XIXe siècle. Des mathématiciens comme Pierre Fatou, Henri Poincaré et Félix Klein ont exploré les comportements complexes des fonctions holomorphes et des transformations itératives.
Mais dès les années 1910, son travail s’inscrit dans la recherche sur les fonctions itératives et l’étude des comportements complexes, dans un contexte difficile sur le sol européen.
La dynamique holomorphe est une nouvelle classe mathématique née des travaux de Gaston Julia et Pierre Fatou sur les fonctions rationnelles complexes. Elle étudie le comportement des suites itératives dans le plan complexe, révélant des structures fractales. Cette discipline a ouvert des perspectives en analyse complexe et en systèmes dynamiques.
Bien que Julia ait publié ses résultats en 1918, ses découvertes sont restées relativement obscures jusqu'à leur redécouverte dans les années 1970 grâce aux avancées informatiques, et notamment le rôle de Benoît Mandelbrot qui a théorisé son ensemble de Mandelbrot, sur la base des théories de Julia.
De plus, Julia est un scientifique controversé en raison des accusations de collaboration en France durant la Seconde guerre mondiale, ce qui a mené de nombreux universitaires à l'exclure des cercles scientifiques.
Dans tous les cas, l'ensemble de Julia reste fondateur dans les mathématiques appliquées modernes. Retour sur l'ensemble de Julia et l'équation correspondante !
L’ensemble de Julia, une équation aux formes infinies
Si des objets comme le flocon de Koch peuvent être étudiés dans le cadre des mathématiques appliquées, l'ensemble de Julia se focalise sur des ensembles plus larges. Ces derniers répondent à la fonction itérative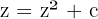 
et de son lien avec la dynamique complexe, ce qui donne naissance à des objets mathématiques infiniment détaillés.
L'ensemble est défini par les points qui restent dans une zone limitée sous l'itération de la fonction :
- Selon les valeurs de
, l'ensemble de Julia peut être soit complexe et connecté, soit fractal et séparé - En fonction des valeurs de , l'ensemble de Julia présente des formes infiniment variées, allant des structures simples aux motifs extrêmement détaillés et visuellement hypnotiques
On dénombre 4 grands principes de l'ensemble de Julia :
- Forme mathématique : L’équation de Julia repose sur l’itération de la fonction quadratique complexe, où ses facteurs sont des nombres complexes.
- Divergence ou stabilité : En appliquant cette fonction de manière répétée à un point
, on observe s’il tend vers l’infini (divergence) ou reste dans une zone limitée (stabilité). - Définition de l’ensemble : L’ensemble de Julia est formé par les points dont les itérations ne divergent pas. Sa forme dépend du paramètre .
- Lien avec Mandelbrot : L’ensemble de Mandelbrot classe les valeurs de selon la stabilité de leur ensemble de Julia, reliant ainsi les deux structures fractales.
Tandis que l’ensemble de Mandelbrot explore les comportements de cette équation en fonction des paramètres complexes, l’ensemble de Julia se concentre sur les résultats obtenus pour des valeurs fixes de ces paramètres. En d’autres termes, chaque point de l’ensemble de Mandelbrot correspond à un ensemble de Julia unique, et les deux ensembles partagent des motifs fractals similaires mais présentent des structures visuelles différentes.
Images hypnotiques et complexes des fractales
Les ensembles de Julia génèrent des images fascinantes, souvent comparées à des œuvres d'art naturelles en raison de leurs structures organiques et infinies, comme on peut le voir dans des fractales végétales ou géologiques. Un exemple concret d'une fractale de Julia n'est autre que le corail marin, qui mêle irrégularité et finesse.
L'ensemble poursuit l'équation suivante :
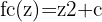
Ces formes se classent en deux grandes catégories :
Les ensembles connexes
Les ensembles totalement disjoints
Ainsi :
- Si c appartient à l’ensemble de Mandelbrot, alors l’ensemble de Julia correspondant est connexe, formant une structure continue. Ces ensembles affichent des formes filamenteuses et riches en détails, rappelant des figures organiques comme des coraux ou des nervures de feuilles. Par exemple, pour
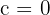, l’ensemble de Julia est un simple disque, tandis que pour des valeurs complexes, il adopte des formes plus tourmentées. - Si c n’appartient pas à l’ensemble de Mandelbrot, alors l’ensemble de Julia est totalement disjoint, composé d’un nuage de points séparés, formant ce que l’on appelle une "poussière de Fatou". Ces ensembles présentent des structures éparses où chaque point est isolé des autres.
Les ensembles de Julia sont extrêmement sensibles aux variations de . Une légère modification entraîne des transformations spectaculaires, donnant naissance à des spirales, des structures arborescentes ou des motifs aux ramifications infinies.
Grâce aux calculs informatiques, il est possible de visualiser ces structures avec un niveau de détail vertigineux, révélant des motifs autosimilaires à chaque niveau de zoom.
Découvrez dès maintenant les applications concrètes de l'ensemble de Julia !
De la théorie aux applications concrètes de l'ensemble de Julia
Notamment du fait de la redécouverte des travaux de Julia par Mandelbrot et d'autres chercheurs, ces derniers ont pu contribuer à l'approfondissement des connaissances en dynamique complexe.
En étudiant les ensembles de Julia, ils ont élargi la compréhension des systèmes non linéaires et de leur comportement chaotique, notamment en informatique, en modélisation scientifique et dans des domaines artistiques, renforçant leur importance dans divers secteurs.
Voici une présentation des utilisations de l’ensemble de Julia en art numérique, en modélisation et en science. Au-delà d'autres objets fractals comme le triangle de Sierpinski, qui n'a plus de secrets depuis sa popularisation dans les salles de classe de technologie, Julia a inspiré bien d'autres réalisations.
Les images fractales jouent un rôle majeur dans plusieurs domaines artistiques et technologiques :
- En art numérique, elles sont utilisées pour créer des œuvres visuelles hypnotiques et complexes, où les motifs se répètent à l’infini avec une richesse de détails fascinante. Les artistes exploitent les propriétés d’auto-similarité pour générer des textures uniques et dynamiques.
- Dans le graphisme, les fractales servent à concevoir des motifs de fond, des textures organiques et des éléments visuels captivants, notamment pour le web design, la mode ou l’illustration. Leur capacité à imiter des formes naturelles comme les nuages ou les branches leur confère un attrait particulier.
- Le cinéma et l’animation exploitent également ces structures mathématiques. Des films de science-fiction et de fantasy intègrent des fractales dans la conception des paysages extraterrestres ou des effets spéciaux. Des logiciels comme Houdini ou Mandelbulb3D permettent de générer des environnements ultra-détaillés à partir d’équations fractales, offrant une esthétique à la fois réaliste et surnaturelle.
soit un chiffre incommensurable
Plus récemment, les ordinateurs jouent un rôle essentiel dans la visualisation des ensembles de Julia, permettant d’explorer leur complexité avec une précision inédite. Grâce aux avancées technologiques, les chercheurs peuvent générer des images haute résolution, révélant des détails infiniment petits qui seraient impossibles à tracer à la main.
Les algorithmes modernes permettent de zoomer profondément dans ces structures, révélant des motifs auto-similaires qui se répètent à différentes échelles. Avec des logiciels comme Ultra Fractal ou Mandelbrot Explorer, il est possible de naviguer dans ces paysages mathématiques et d’en découvrir la richesse cachée.
Enfin, l’intelligence artificielle et le calcul haute performance ont également amélioré la génération de ces images. Les fractales ne sont plus de simples curiosités mathématiques, elles sont devenues des outils d’étude et d’inspiration pour les sciences, l’art et la technologie. Cela signifie que l’informatique a permis de rendre accessibles ces objets abstraits et fascinants au grand public.
Maintenant que vous savez tout sur l'ensemble de Julia, vous pouvez vous entraîner à visualiser des fractales grâce aux logiciels informatiques !
Vous avez aimé cet article ? Notez-le !
Loading...
