En matière de fractales, le triangle de Sierpinski est un incontournable pour comprendre les fractales. Découvert par Wacław Sierpiński en 1915, il illustre des concepts fondamentaux des mathématiques et trouve des applications en biologie, en physique et en informatique. Sa simplicité apparente cache une richesse géométrique aux implications profondes.
Voici tout ce qu'il faut savoir sur cette forme particulière : c'est parti !
Comprendre ce qu'est un triangle de Sierpinski
Le triangle de Sierpinski est une fractale découverte en 1915 par le mathématicien polonais Wacław Sierpiński. Sa construction repose sur un processus itératif simple, qui peut être réalisé à la main ou à l’aide d’un programme informatique.
D’un point de vue mathématique, le triangle de Sierpinski illustre des propriétés fondamentales des fractales, dans la lignée d'autres théories comme l'ensemble de Julia, pionnier en la matière. Il est auto-similaire, ce qui signifie que n’importe quelle partie de la figure est une réplique réduite de l’ensemble.
Sa dimension fractale n’est pas entière, contrairement aux objets géométriques classiques, et elle est calculée par la relation suivante :
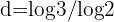, soit environ 1,58 = c'est la dimension de Hausdorff
Grâce à son apparence identique à différentes échelles, le triangle de Sierpinski est un excellent exemple de l’invariance d’échelle en géométrie fractale :
- Son motif se retrouve dans la nature et en science, notamment dans la modélisation des réseaux ou l’étude des systèmes dynamiques
- Il est souvent utilisé en informatique pour illustrer la récursivité, et sa construction peut être programmée avec des algorithmes basés sur la répétition de règles simples
Wacław Sierpiński (1882-1969) était un mathématicien polonais connu pour ses contributions en théorie des ensembles, topologie et géométrie fractale. Il a présenté des structures connues comme comme le triangle et le tapis de Sierpinski, qui illustrent l’auto-similarité. Son travail a influencé la théorie fractale et trouvé des applications en informatique, physique et modélisation mathématique.
Cette simplicité apparente cache une richesse mathématique qui continue d’intriguer chercheurs et passionnés de géométrie, mais aussi de biologie. On vous explique pourquoi ci-dessous.
Le triangle de Sierpinski, un algorithme entre maths et biologie
Le triangle est utile en mathématiques pour illustrer l’auto-similarité et la dimension fractale non entière, concepts fondamentaux en géométrie fractale.
En biologie, il aide à modéliser des structures naturelles comme les réseaux vasculaires, les motifs de croissance des plantes ou l’organisation cellulaire.
Cela offre une meilleure compréhension des processus d’optimisation et d’auto-organisation dans le vivant.
Les algorithmes permettant de construire le triangle de Sierpinski sont basés sur des règles simples d’itération et de division, ce qui les rend accessibles même à ceux qui ne sont pas experts en mathématiques.
Il existe plusieurs méthodes pour générer cette fractale, mais deux des plus courantes sont :
La méthode de suppression des triangles
La méthode du chaos
Méthode de suppression des triangles
La méthode de suppression des triangles pour construire le triangle de Sierpinski repose sur une approche itérative :
- On commence avec un triangle équilatéral de côté
- À la première étape, on relie les milieux de ses côtés pour former quatre sous-triangles équilatéraux plus petits, chacun de côté
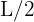
- On enlève ensuite le triangle central, laissant trois sous-triangles équilatéraux restants.
À l’étape suivante, on applique le même processus à chacun des trois sous-triangles conservés. On divise encore chaque côté par deux, on retire les nouveaux triangles centraux, et ainsi de suite. Après 
itérations, le nombre de triangles restants est donné par la formule 
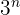, tandis que la longueur totale du périmètre augmente exponentiellement avec 
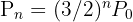, où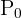 
est le périmètre initial.
Une propriété clé de cette construction est sa dimension fractale, qui est donnée par la formule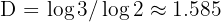 
, une valeur non entière caractéristique des objets fractals.
En poursuivant ce processus indéfiniment, on obtient une structure infiniment ajourée où l’aire tend vers zéro, bien que le périmètre continue d’augmenter, illustrant le paradoxe géométrique des fractales.
Méthode du jeu de chaos
La méthode du "jeu du chaos" est une approche probabiliste surprenante pour générer le triangle de Sierpinski :
- Elle commence avec un triangle équilatéral défini par trois sommets fixes
,
, 
- Un point initial 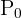est choisi aléatoirement à l’intérieur de ce triangle
- À chaque étape, on sélectionne au hasard l’un des trois sommets et on place un nouveau point à mi-chemin entre le point actuel et ce sommet choisi
Mathématiquement, si 
est la position actuelle du point, et si 
est le sommet choisi au hasard, alors la nouvelle position du point est donnée par la relation :
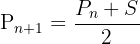
En répétant ce processus un grand nombre de fois, la figure du triangle de Sierpinski émerge progressivement. Ce phénomène repose sur la convergence stochastique et l’auto-similarité des fractales. Bien que chaque placement soit basé sur un choix aléatoire, l’accumulation de ces itérations génère une structure géométriquement ordonnée.
Une explication intuitive de ce résultat réside dans l’auto-similarité. En effet, chaque région du triangle respecte la même règle de formation à toutes les échelles. Le jeu du chaos illustre comment des processus aléatoires peuvent produire des motifs déterministes, une propriété qui trouve des applications en physique, biologie et informatique.
Le triangle de Sierpiński partage des similitudes avec d’autres fractales célèbres, qui ont des applications en mathématiques et en biologie. Tout comme l’ensemble de Mandelbrot ou le flocon de Koch, il est construit par un processus itératif et possède une dimension fractale non entière. Cependant, chaque fractale possède des particularités :
- L’ensemble de Mandelbrot illustre des dynamiques complexes
- Le flocon de Koch représente une courbe infiniment longue délimitant une surface finie
Ces liens entre mathématiques et nature font du triangle de Sierpinski un objet intéressant, révélateur des structures cachées qui régissent le monde naturel.
Des applications surprenantes : réseaux et télécommunications
Le triangle de Sierpinski a servi de base d'inspiration pour de nombreuses applications, que ce soit dans les télécommunications, les réseaux ou la nature.
Les antennes fractales, grâce à leur forme auto-similaire, peuvent capter des signaux sur plusieurs fréquences simultanément, améliorant ainsi la réception et la transmission des signaux. Cela est particulièrement utile dans les télécommunications modernes, où l’efficacité et la capacité de fonctionner sur différentes bandes de fréquence sont cruciales pour garantir des communications stables et rapides.
Dans le domaine des réseaux, la structure fractale du triangle de Sierpinski est exploitée pour optimiser les systèmes de distribution de données, à l'image de la fractale du flocon de Koch. En utilisant des algorithmes inspirés de la géométrie fractale, il est possible de concevoir des réseaux plus efficaces, où les données peuvent être distribuées de manière optimale, en réduisant les risques de congestion et d’interférences.
Le triangle de Sierpinski trouve aussi des analogies frappantes dans la nature, notamment dans les motifs des fougères et de certains coquillages. Ces structures naturelles suivent des principes de croissance fractale similaires, où une forme globale se répète à des échelles de plus en plus petites :
🌿 Les fougères, par exemple, présentent des frondes constituées de plus petites frondes identiques, illustrant parfaitement l’auto-similarité fractale
🐚 Certains coquillages, comme ceux des nautiles, adoptent des formes géométriques qui rappellent l’organisation du triangle de Sierpinski
Cette fractale joue également un rôle en biologie, notamment dans l’étude des modèles d’organisation cellulaire et des réseaux vasculaires :
- Les vaisseaux sanguins ou les structures neuronales adoptent des schémas de ramification qui optimisent la répartition des ressources, une propriété également observée dans la construction du triangle de Sierpinski
- En biologie du développement, on retrouve des modèles de division cellulaire qui se rapprochent de ce principe fractal, témoignant de son importance dans la compréhension des formes vivantes
Ce sont là des applications variées et particulièrement modernes. Mais bien au-delà, le triangle de Sierpinski inspire aussi en graphisme, en informatique et jusque dans les jeux vidéo.
Inspirations visuelles du serpent de Sierpinski
L'influence des fractales, et en particulier du triangle de Sierpinski, dans l'art et le graphisme est significative.
Ces motifs géométriques ont inspiré de nombreux artistes et designers qui explorent la beauté des formes auto-similaires et infinies, y compris dans la nature.
Que ce soit avec des fractales triangulaires présentes dans la nature ou d'autres fractales mathématiques comme le flocon de Koch, le triangle de Sierpinski est source d'inspiration à de nombreuses échelles.
Dans l'art, les fractales apportent une dimension unique de répétition, de symétrie et de complexité, tout en conservant une harmonie visuelle. De nombreux artistes contemporains, notamment dans les domaines du graphisme numérique et de l'art visuel, utilisent des fractales comme base de leurs créations. L’aspect répétitif des formes fractales génère un effet hypnotique et intrigant qui capte l’attention du spectateur.
Les fractales ont également trouvé une place de choix dans le monde de l'animation et des jeux vidéo. Dans ces industries, la capacité des fractales à modéliser des environnements et des effets visuels complexes de manière efficace est cruciale.
Par exemple, la génération procédurale de terrains et de paysages dans les jeux vidéo utilise des algorithmes fractals pour créer des paysages naturels réalistes. L'usage des fractales permet de concevoir de vastes environnements avec une économie de ressources, en produisant des détails infiniment complexes tout en optimisant le processus de rendu informatique
Dans l'animation, les fractales sont également utilisées pour générer des effets visuels spectaculaires, comme des explosions, des flammes ou des phénomènes naturels comme les tornades. Leur capacité à modéliser des phénomènes complexes et dynamiques les rend indispensables dans la création d'effets spéciaux modernes.
Et vous, quelles sont vos applications ou modélisations préférées du triangle de Sierpinski ?
Vous avez aimé cet article ? Notez-le !
Loading...
