Chapitres

L'énergie cinétique

Tout corps en mouvement en possède une. Elle peut être macroscopique : elle dépend alors de la vitesse du corps en mouvement, et donc du référentiel d'étude microscopique : elle est liée à l'agitation moléculaire. Une augmentation de l'énergie cinétique microscopique se traduit par une augmentation de la température.
En résumé, l'énergie cinétique correspond à l'énergie d'un objet en mouvement.
La formule est : 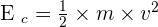
Avec :
- Ec correspondant à l'énergie cinétique de l'objet étudié avec pour unité le Joule noté J ;
- m correspondant à la masse de l'objet étudié avec pour unité le kilogramme noté kg ;
- Et v correspondant à la vitesse de l'objet étudié avec pour unité la mètre par seconde noté m.s-1.
Exemple
Prenons le cas d'un système en translation. Il est important de savoir que la relation définissant l'énergie cinétique ne s'applique pas pour les solides en rotation. Exemple : L'énergie cinétique d'une voiture qui pèse 1 tonne et qui roule à 130 Km/h est de 
La vitesse
La vitesse est une grandeur physique qui est définie par une évolution face au temps. La vitesse ne définit pas qu’uniquement la vitesse de déplacement mais peut aussi correspondre à la vitesse de réaction chimique ou encore une vitesse de séchage par exemple. En règle générale, une vitesse est égale à la division de la mesure d’une variation telle qu’une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation. L’exemple le plus simple est celui de la vitesse de déplacement. Il s’agit d’une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.
La masse
En physique, la masse correspond à une grandeur physique positive et intrinsèque d'un corps. De façon plus précise, en physique newtonienne, la masse correspond à une grandeur extensive. Cela signifie alors que la masse d'un corps formé de parties correspond à la somme des masses de ces différentes parties qui le compose. De plus, il est essentiel de noter que la masse est une grandeur conservative. De ce fait, elle reste constante dans le cas d'un système isolé qui n'échange donc pas de matière avec son environnement.
L'énergie potentielle (ou de position)

Elle dépend de la position relative des différentes parties du système: seul un systèmes déformable pourra posséder, à l'échelle macroscopique, de l'énergie potentielle.
En résumé, l'énergie potentielle correspond à l'énergie contenue dans un objet au dessus du sol.
La formule est : 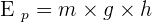
- Ep correspondant à l'énergie potentielle de l'objet étudié avec pour unité le Joule noté J ;
- m correspondant à la masse de l'objet étudié avec pour unité le kilogramme noté kg ;
- g correspondant à l'intensité de pesanteur avec pour unité le Newton par kilogramme noté N.kg-1. A noter que la valeur approximative de g est de 9,81 N.kg-1.
- Et v correspondant à la vitesse de l'objet étudié avec pour unité la mètre par seconde noté m.s-1.
Gravitation et champ gravitationnel

Définition : La gravitation correspond à une force attractive qui s'exerce à distance entre deux corps qui ont une masse.
Cette force dépend :
- de la distance: Plus la distance est grande, plus la force est petite.
- de la masse des corps: Plus la masse est grande, plus la force gravitationnelle est grande.
Le champ gravitationnel peut être comparé à un champ électrique
En physique classique, on appelle champ gravitationnel, ou encore champ de gravitation, un champ qui est réparti dans l'espace et dû à la présence d'une masse qui est alors susceptible d'exercer une influence gravitationnelle sur tout les autres corps pouvant être présent à proximité immédiate ou non. On peut démontrer que le champ gravitationnel créé en un point quelconque par un corps ponctuel dérive d'un potentiel scalaire dit newtonien. En physique classique, le champ gravitationnel ou champ de gravitation est un champ réparti dans l'espace et dû à la présence d'une masse susceptible d'exercer une influence gravitationnelle sur tout autre corps présent à proximité (immédiate ou pas). L'introduction de cette grandeur permet de s'affranchir du problème de la médiation de l'action à distance apparaissant dans l'expression de la force de gravitation universelle. On peut interpréter le champ gravitationnel comme étant la modification de la métrique de l'espace-temps. L'approximation newtonienne est alors valable uniquement dans le cas où les corps présentent une vitesse faible par rapport à celle de la lumière dans le vide et si le potentiel gravitationnel qu'ils créent est tel que le quotient du potentiel gravitationnel sur le carré de la vitesse de la lumière dans le vide est négligeable. On peut approcher le champ électrique et le champ gravitationnel. En effet, l'expression du champ et du potentiel ne sont différents que d'une constante. De plus, les principaux théorèmes de calculs, celui de la superposition ou de Gauss par exemple, peuvent s'appliquer dans les deux cas. Ce qui les différencie alors est le caractère attractif, donc entre deux charges de signe opposé, ou répulsif, donc entre deux charges de même signe, du champ électrique tandis que le champ gravitationnel ne peut être qu'attractif.
Le principe de l'analogie
- L'analogie repose sur la similitude des lois de Coulomb (électromagnétisme) et loi de Newton (gravitation).
- Il est souvent inutile de faire les calculs de champs gravitationnels à partir de répartitions de masses, on procède plutôt par analogie avec les résultats connus de l'électrostatique.
La force d'interaction gravitationnelle, tout comme la force d'interaction électrostatique, est une force conservative. Ainsi, elles représentent toutes les deux le gradient d'une énergie potentielle. Dans ce cas, il est alors possible d'adapter absolument tous les calculs de champ et de potentiel étudiés dans le cadre du cours sur la distribution de masses dans le but de calculer le champ et le potentiel gravitationnels en un point définis de l'espace. Il en va de même avec le théorème de Gauss.
Remarque
Il peut être intéressant de mentionner que la force électrique fondamentale, également appelée force de Coulomb, peut être utilisée comme fondement de l'électrostatique. Ainsi, on peut déduire de ce fondement le théorème de Gauss. C'est donc pour cela que l'on peut dire que la ressemblance formelle, c'est-à-dire les similarité des formules mathématiques, entre la force de Coulomb et la force gravitationnelle est une base solide permettant de fonder l'analogie entre les deux classes de phénomènes énoncés dans ce cours. Ainsi, à partir de la force de Coulomb et par superposition, on peut être capable d'établir des expressions intégrales du champ électrique en fonction de la distribution de charge. Bien que ces calculs soient trop complexes pour être utiles dans les calculs analytiques, ils peuvent être très utiles afin de déterminer un champ électrique par résolution numérique, c'est-à-dire par ordinateur. Notons qu'il est possible de démontrer ces formules en utilisant le théorème de superposition.
A titre comparatif
Champ électrique
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance. Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi : 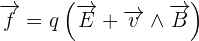 avec :
avec :
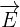 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge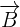 le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude. Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes. Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb. On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet. Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électrostatique
On parle de champ électrostatique lors que les charges qui constitue le champ sont au repos dans le référentiel d'étude. Ce champ est donc déduit de l'expression de la loi de Coulomb, aussi appelée interaction électrostatique. En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen. On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante : 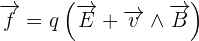 avec :
avec :  le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge  le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi. En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude. De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante. D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi. En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude. De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante. D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
L'énergie mécanique
L'énergie mécanique Em d'un système est une grandeur macroscopique, somme de son énergie cinétique Ec et de son énergie potentielle Ep. 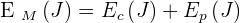 L'énergie mécanique dépend alors du référentiel d'étude.
L'énergie mécanique dépend alors du référentiel d'étude.
Etude des différentes énergies dans un cas concret de chute

Un système isolé est rigoureusement un système qui n'échange ni matière, ni énergie avec l'extérieur. L'énergie totale d'un système isolé est donc constante.
Rappel : Les différentes formes d'énergie du système sont l'énergie potentielle de pesanteur (notée Ep) et l'énergie cinétique (notée Ec). Leur somme correspond à l'énergie mécanique (notée Em).
Prenons l'exemple de la chute libre d'une bille.
- Avant la chute, le système possède une énergie potentielle Ep mais aucune énergie cinétique Ec=0 car la vitesse est nulle dans le référentiel terrestre.
- Au cours de la chute, l'énergie potentielle Ep diminue car l'altitude de la bille par rapport au sol diminue, tandis que l'énergie cinétique augmente car la vitesse de la bille augmente.
- Au sol, l'énergie potentielle Ep = 0 tandis que l'énergie cinétique est maximale.
On peut donc dire que les différentes formes d'énergie se transforment les unes en les autres. Si l'énergie totale du système n'est pas constante, le système n'est pas isolé. En l'absence de frottement le système est isolé soit : 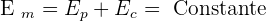
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Je valide ce document fort qualitatif
C’est très intéressant le cours
merci
Oui