Chapitres

La résistance électrique dans un circuit

La résistance désigne la capacité physique d'un matériau à s'opposer au passage d'un courant électrique sous une certaine tension. C'est de là que sont nés les composants électriques appelés les résistances. Lorsqu'on insère différents matériaux (du graphite puis du cuivre, par exemple) dans un petit circuit électrique contenant une lampe, on constate que la lampe ne brille pas du même éclat. Le courant électrique est plus intense avec le cuivre qui est donc un meilleur conducteur. Cela signifie que le graphite s'oppose plus au passage du courant dans le circuit que le cuivre. On dit que ces deux matériaux ne possèdent pas la même résistance au passage du courant. De manière générale, tous les conducteurs possèdent une propriété qui s'appelle la résistance électrique : celle-ci traduit la capacité de s'opposer plus ou moins au passage du courant. Ainsi, la résistance du cuivre étant plus faible que celle du graphite, c'est un meilleur conducteur. Remarque : dans la vie courante, nous sommes souvent confrontés à d'autres types de résistance. Ainsi lorsqu'on nage contre le courant, la mer s'oppose à notre progression. Elle exerce une résistance à notre avancée. On sait déjà mesurer l'intensité du courant et la tension électrique mais comment peut-on mesurer cette nouvelle grandeur : la résistance électrique ?
Mesurer la résistance

Une résistance est habituellement représentée par un rectangle et se note R, K ou M selon sa capacité. R représente les ohms, K les kiloohms et pour finir, M les Megaohms selon le Système International. Un code couleur est appliqué sur les résistances afin de connaître leur valeur. Voici un tableau qui regroupe toutes les couleurs et la nomenclature des résistances :
| Premier anneau de gauche | Deuxième anneau de gauche | Troisième anneau de gauche | Dernier anneau de gauche | Anneau de droite | |
|---|---|---|---|---|---|
| Couleur | Premier chiffre | Deuxième chiffre | Troisième chiffre | Multiplicateur | Tolérance |
| Absent | 20 % | ||||
| Argent | 10-2 | 10 % | |||
| Or | 10-1 | 5 % | |||
| Noir | 0 | 0 | 0 | 1 | 20 % |
| Marron | 1 | 1 | 1 | 10 | 1 % |
| Rouge | 2 | 2 | 2 | 102 | 2 % |
| Orange | 3 | 3 | 3 | 103 | |
| Jaune | 4 | 4 | 4 | 104 | |
| Vert | 5 | 5 | 5 | 105 | 0,5 % |
| Bleu | 6 | 6 | 6 | 106 | 0,25 % |
| Violet | 7 | 7 | 7 | 107 | 0,10 % |
| Gris | 8 | 8 | 8 | 108 | 0,05 % |
| Blanc | 9 | 9 | 9 | 109 |
Résistance et unité
L’ensemble des unités associées aux dimensions fondamentales constitue le système international d’unités. Il s’agit du système MksA (mètre, kilogramme, seconde, Ampère), mais le Kelvin, le mole et le candela font aussi partie de ce système. Ces unités sont appelées unités légales. Elles sont universelles et connues par le monde entier. Il est important de savoir que toutes les autres dimensions se déduisent de ces sept dimensions fondamentales par produit ou division de ces dimensions. Dans certains sujets d’exercices, les grandeurs ne sont pas exprimées dans le système international mais avec des grandeurs usuelles. Il est facile de les comprendre et elles sont parfois utilisées dans la vie de tous les jours, mais il est essentiel de toujours effectuer les calculs avec les grandeurs exprimées dans l’unité internationale pour éviter les erreurs. Pour mesurer la résistance d'un conducteur, on utilise un ohmmètre. Il faut simplement placer cet appareil aux bornes du conducteur en dehors de tout circuit. Si on effectue un certain nombre de mesures, on constate que les matériaux présentent des résistances de valeurs extrêmement diverses. Exemples : Un morceau de cuivre a une résistance de l'ordre de quelques centièmes d'ohms tandis que la résistance d'une mine de crayon en graphite est de l'ordre de 10 ohms. La résistance du corps humain sec a une valeur de l'ordre de 1 megaohm tandis que si nous sommes mouillés, la valeur est environ divisée par un facteur 2 (Ces valeurs diffèrent selon les personnes !). Si on cherche à mesurer la résistance d'un isolant (comme le bois sec, la laine, le verre, etc.), l'ohmmètre ne peut donner aucune valeur, ce qui signifie que les isolants ont une résistance très grande.
La résistance dans un circuit : les effets
Nous venons de voir que la résistance du cuivre était bien inférieure à celle du graphite (mine de crayon). On peut maintenant interpréter l'expérience de la façon suivante : la lumière brille plus avec le cuivre parce que la valeur de sa résistance est beaucoup plus faible. En généralisant, on obtient le résultat suivant : plus la résistance dans un circuit augmente, plus l'intensité du courant électrique dans ce circuit diminue. Ce résultat a de nombreuses applications : Dans des circuits électroniques, on utilise souvent des résistances pour limiter l'intensité du courant. Les bagues colorées dont elles sont cerclées indiquent, grâce à un code de couleurs, la valeur approximative de la résistance. Pour faire varier le volume sonore des baladeurs, on fait varier la résistance du circuit qui alimente le haut-parleur. Une résistance peut être composée de divers matériaux selon qu'elle soit de faible ou haute puissance. Par exemple, les résistances de moins de 2 W sont constituées de carbone et de céramique. Ce type de résistance a pour avantage de générer très peu de bruit thermique, ce qui en fait un élément de choix dans les circuits audio. Les résistances faites pour supporter des puissances supérieures seront quant à elles fabriquées à l'aide d'un cylindre de céramique sur lequel sera enroulé un fil conducteur. Pour finir, les résistances à très hautes puissance sont constituées de solution aqueuse contenant des ions cuivre et qui ralentissent grandement le passage du courant électrique.
La puissance électrique dans un circuit

La puissance électrique, très souvent notée P, possède pour unité le watt, de symbole W. Elle correspond au produit de la tension électrique, donc en volts, aux bornes de laquelle on branche l'appareil avec l'intensité du courant électrique, donc en ampères, qui va donc traverser l'appareil. Notez que ceci est vrai pour les appareils qui sont purement résistifs.
La puissance en régime continu
Lorsque la tension et le courant sont continu, on définit la puissance avec la formule suivante : 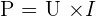 Avec U et I des valeurs constantes de la tension aux bornes du dipôle et de l'intensité du courant à travers le dipôle. Notons que si l'on considère R comme étant la résistance du dipôle, on a :
Avec U et I des valeurs constantes de la tension aux bornes du dipôle et de l'intensité du courant à travers le dipôle. Notons que si l'on considère R comme étant la résistance du dipôle, on a :  On obtient donc en définitive la formule de calcul de la puissance suivante :
On obtient donc en définitive la formule de calcul de la puissance suivante :  Il est possible de modéliser un dipôle actif linéaire, donc un électromoteur, avec un modèle équivalent de Thévenin même si ce modèle, très sommaire, ne permet pas de rendre compte des éventuelles chutes de tension en charge ou encore des puissances électriques mises en jeu dans un domaine de validité qu'il faut nécessairement préciser. Ainsi, convention générateur, la puissance fournie par le dipôle à l'extérieur peut s'exprimer de la façon suivante :
Il est possible de modéliser un dipôle actif linéaire, donc un électromoteur, avec un modèle équivalent de Thévenin même si ce modèle, très sommaire, ne permet pas de rendre compte des éventuelles chutes de tension en charge ou encore des puissances électriques mises en jeu dans un domaine de validité qu'il faut nécessairement préciser. Ainsi, convention générateur, la puissance fournie par le dipôle à l'extérieur peut s'exprimer de la façon suivante : 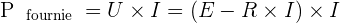
 La puissance fournie par le dipôle actif correspond alors à la puissance fournie par un générateur idéal de tension, noté E, qui va donc délivrer un courant, noté I, dont une partie est dissipée par effet Joule, représenté par -RxI2 . Si on se concentre sur le cas des moteurs électriques, ExI est un terme représentant la puissance électromécanique que l'on note Pem.
La puissance fournie par le dipôle actif correspond alors à la puissance fournie par un générateur idéal de tension, noté E, qui va donc délivrer un courant, noté I, dont une partie est dissipée par effet Joule, représenté par -RxI2 . Si on se concentre sur le cas des moteurs électriques, ExI est un terme représentant la puissance électromécanique que l'on note Pem.
La puissance en régime alternatif
Si la tension et le courant varient, on considère que la puissance instantanée consommée par un dipôle est représentée par le produit des valeurs instantanées du courant qui le traverse et de la tension à ses bornes. On obtient alors la formule suivante : 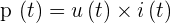 Si on se considère en régime sinusoïdal, on peut exprimer la tension et l'intensité de la façon suivante :
Si on se considère en régime sinusoïdal, on peut exprimer la tension et l'intensité de la façon suivante : 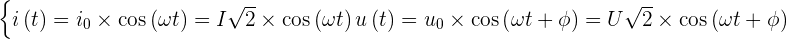 Avec :
Avec :
- U et I sont les valeurs efficaces de la tension et du courant
- Et Φ est le déphasage de la tension par rapport au courant.
On obtient alors l'expression de la puissance suivante : 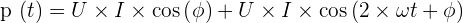 Il peut alors être intéressant de noter que le premier terme de la somme ci-dessus correspond à la puissance active alors que le second terme correspond à la puissance sinusoïdale de fréquence qui est double de celle du courant et de la tension. La position moyenne de cette puissance sinusoïdale est d'ailleurs égale à la puissance active. De plus, la valeur de \cos(Φ) correspond quant à lui au facteur de puissance en régime sinusoïdal. On appelle ainsi puissance fluctuante une puissance sinusoïdale de fréquence double de celle du courant et de la tension. Cette puissance n'a, pour les convertisseurs électrothermiques, aucun effet puisque l'inertie thermique du système permet de lisser et ce de façon totale les variations de puissance. Cependant, cela n'est pas vrai pour les conversions électromécaniques puisque la machine électrique, qu'elle soit moteur ou génératrice, tourne avec une vitesse presque constante grâce à son inertie. De ce fait, à chaque instant elle consomme ou fournit, modulo des pertes, une puissance mécanique identique. Ainsi, la puissance fluctuante est responsable d'oscillations de couples qui sont, pour la majeure partie, absorbée par l'élasticité de l'arbre de transmission. C'est pour cela que, pour une machine de forte puissance, ces oscillations sont à éviter puisqu’elles risquent de provoquer la destruction de cette machine. Cela étant la raison par laquelle les alternateurs de centrales électrique ou encore les très gros moteurs se doivent d'être polyphasés. Dans les faits, ils sont généralement triphasés.
Il peut alors être intéressant de noter que le premier terme de la somme ci-dessus correspond à la puissance active alors que le second terme correspond à la puissance sinusoïdale de fréquence qui est double de celle du courant et de la tension. La position moyenne de cette puissance sinusoïdale est d'ailleurs égale à la puissance active. De plus, la valeur de \cos(Φ) correspond quant à lui au facteur de puissance en régime sinusoïdal. On appelle ainsi puissance fluctuante une puissance sinusoïdale de fréquence double de celle du courant et de la tension. Cette puissance n'a, pour les convertisseurs électrothermiques, aucun effet puisque l'inertie thermique du système permet de lisser et ce de façon totale les variations de puissance. Cependant, cela n'est pas vrai pour les conversions électromécaniques puisque la machine électrique, qu'elle soit moteur ou génératrice, tourne avec une vitesse presque constante grâce à son inertie. De ce fait, à chaque instant elle consomme ou fournit, modulo des pertes, une puissance mécanique identique. Ainsi, la puissance fluctuante est responsable d'oscillations de couples qui sont, pour la majeure partie, absorbée par l'élasticité de l'arbre de transmission. C'est pour cela que, pour une machine de forte puissance, ces oscillations sont à éviter puisqu’elles risquent de provoquer la destruction de cette machine. Cela étant la raison par laquelle les alternateurs de centrales électrique ou encore les très gros moteurs se doivent d'être polyphasés. Dans les faits, ils sont généralement triphasés.
Le lien avec le travail électrique
Un dipôle parcouru par un courant d'intensité I échange de l'énergie avec le reste du circuit. Le mode de transfert est le travail des forces électriques. Pendant la durée t, les forces électriques s'exerçant sur les charges qui traversent un dipôle AB, parcouru par un courant d'intensité I circulant de A vers B effectuent le travail : 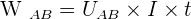 Étant donné la définition de la puissance , il est possible de savoir que la puissance des forces électriques correspond à :
Étant donné la définition de la puissance , il est possible de savoir que la puissance des forces électriques correspond à : 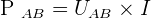 Ainsi, on sait que :
Ainsi, on sait que :
- Si la puissance est positive, alors le dipôle AB a reçu cette puissance.
- Si la puissance est négative, alors le dipôle AB a cédé cette puissance.
Avec :
- La tension U qui s'exprime en volt (V) ;
- L'intensité I qui s'exprime en ampère (A) ;
- Le temps t qui s'exprime en seconde (s) ;
- Le travail W qui s'exprime en joule (J) ;
- Et la puissance P qui s'exprime en watt (W).
On sait que, lorsqu'un dipôle est traversé par un courant, il y a transfert d'énergie entre le dipôle et le milieu ambiant. De ce fait, lorsque le circuit est traversé par un courant d'intensité I, alors peu importe le dipôle présent au sein de ce circuit, celui-ci va s'échauffer. On appelle cela l'effet Joule. De ce fait, le dipôle qui sera ainsi échauffé va céder de l'énergie par chaleur au milieu ambiant. On sait également que lorsqu'il le dipôle est traversé par un courant, alors celui-ci est capable d'effectuer un travail (on le considère alors comme un moteur électrique). Il cède alors de l'énergie au milieu ambiant par travail. Par la même façon, lorsque le dipôle est traversé par un courant, alors celui-ci est capable d'émettre de la lumière (on le considère alors comme lampe électrique). Il cède alors de l'énergie au milieu ambiant. La loi d'ohm s'écrit, pour un courant traversant le conducteur ohmique de A vers B : 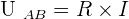 où R est la résistance du conducteur ohmique. Tandis que la loi de Joule s'exprime ainsi :
où R est la résistance du conducteur ohmique. Tandis que la loi de Joule s'exprime ainsi :  Cette puissance est toujours positive. Un conducteur ohmique reçoit de l'énergie du reste du circuit. Le dipôle s'échauffe. Puis sa température reste constante : à chaque instant, l'énergie reçue du reste du circuit par travail des forces électriques est cédée au milieu ambiant par chaleur. La puissance
Cette puissance est toujours positive. Un conducteur ohmique reçoit de l'énergie du reste du circuit. Le dipôle s'échauffe. Puis sa température reste constante : à chaque instant, l'énergie reçue du reste du circuit par travail des forces électriques est cédée au milieu ambiant par chaleur. La puissance  correspond à l'effet Joule.
correspond à l'effet Joule.
Informations complémentaires

La résistance du corps humain
Il est important de savoir que la résistance du corps humain, et donc son opposition au passage du courant, est composée de façon générale par plusieurs autres résistances disposées en série ou en parallèle selon le trajet du courant. On peut alors définir la valeur de la résistance du corps humain en utilisant la loi d'Ohm La résistance du corps humain (c'est-à-dire son opposition au passage du courant) est elle-même composée de plusieurs résistances en série ou en parallèle selon le trajet du courant, défini par la loi d'Ohm.
La variation de la résistance du corps humain
La résistance du corps humain, ou encore son impédance, peuvent varier selon différents facteurs qui sont :
- Le trajet du courant et, de façon plus précise, les points de contacts
- La surface de contact cutanée ainsi que la surface de section des structures qui vont être traversée par le courant. En effet, puisque la résistance est inversement proportionnelle à cette surface, plus la surface est petite, plus la résistance sera importante.
- Les temps de contact : plus la durée de contact avec le courant est élevée, plus les lésions seront profondes et graves
- L'état de la surface de contact. En effet, plus la peau est fine et humide, plus la résistance va diminuer. Par exemple, une peau épaisse, sèche est de 2 . 106 Ω contre 500 Ω pour une peau fine et humide.
Pour ce qui est des tissus biologiques, leur résistance est variable bien que généralement faible. De plus, si le tissu brûle, alors sa résistance augmente.























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Salut j’ai trouvé le document intéressant mais s’il vous plaît, j’aimerais savoir comment differencier physiquement les résistance de puissance des résistances de faibles puissance.