Chapitres

L'énergie électrique notée E

On appelle énergie électrique toute énergie étant transférée ou encore stockée grâce à l'électricité. Très souvent, cette énergie est transférée d'un système à un autre système via des mouvements de charges. Il existe de nombreux systèmes capable de fournir de l'énergie par transfert électrique. On peut d'ailleurs nommer les alternateurs ou les systèmes chimiques comme les piles. Les systèmes capables de transformer de l'énergie issue de l'électricité en un autre type d'électricité sont :
- Les résistances électrique qui transforment l'énergie électrique en chaleur ;
- Les moteurs qui transforment l'énergie électrique en un travail mécanique ;
- Les lampes qui transforment l'énergie électrique en rayonnement lumineux et en chaleur ;
- Ou encore les systèmes électrotechniques ou les systèmes électroniques.
Le transport de l'énergie électrique, quant à elle, peut se faire grâce à l'utilisation d'un conducteur électrique comme le métal ou encore une solution ionique. L'inconvénient de l'énergie électrique, c'est qu'elle ne peut pas être stockée en grande quantité. En effet, nous ne sommes en mesure de stocker que de petites quantité de charges électriques sous forme d'énergie appelée électrostatique. Dans ce cas, on utilise couramment des condensateurs. En électricité, il n'est pas correct de parler d'énergie électrique. En effet, cette expression représente plutôt une commodité de langage permettant de signaler que l'électricité nécessite mais transporte également de l'énergie. Pour stocker de l'énergie qui a été fournie via un transfert électrique, il est nécessaire de faire appel à un convertisseur qui est capable de stocker l'énergie reçue sous la forme d'énergie chimique comme c'est le cas avec les accumulateur ou sous la forme d'énergie mécanique ou potentielle comme cela peut être le cas dans une STEP ou un barrage hydro-électrique.
Remarque sur la résistance

| Premier anneau de gauche | Deuxième anneau de gauche | Troisième anneau de gauche | Dernier anneau de gauche | Anneau de droite | |
|---|---|---|---|---|---|
| Couleur | Premier chiffre | Deuxième chiffre | Troisième chiffre | Multiplicateur | Tolérance |
| Noir | 0 | 0 | 0 | 1 | 20 % |
| Marron | 1 | 1 | 1 | 10 | 1 % |
| Rouge | 2 | 2 | 2 | 102 | 2 % |
| Orange | 3 | 3 | 3 | 103 | |
| Jaune | 4 | 4 | 4 | 104 | |
| Vert | 5 | 5 | 5 | 105 | 0,5 % |
| Bleu | 6 | 6 | 6 | 106 | 0,25 % |
| Violet | 7 | 7 | 7 | 107 | 0,10 % |
| Gris | 8 | 8 | 8 | 108 | 0,05 % |
| Blanc | 9 | 9 | 9 | 109 | |
| Or | 10-1 | 5 % | |||
| Argent | 10-2 | 10 % | |||
| Absent | 20 % |
La relation entre la puissance et l'énergie dans le cas d'un régime permanent

Dans le cas de l'énergie électrique, l'apport d'énergie est proportionnel à la quantité d'électricité. On peut illustrer cela avec la relation suivante : 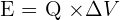 Où :
Où :
- L'énergie, notée E, en joules ;
- La charge, notée Q, en coulombs ;
- Et la différence de potentiel aux bornes de l'appareil, notée ΔV, en volts.
Et avec  la quantité d'électricité peut se quantifier avec la formule suivante :
la quantité d'électricité peut se quantifier avec la formule suivante : 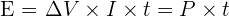 Où :
Où :
- P représente la puissance en watts ;
- Et t représente la durée en secondes.
L'énergie électrique notée E consommée par un appareil de puissance P pendant une durée t est donnée par les relation :
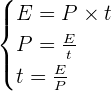
Où :
- P, la puissance est exprimée en Watt ;
- E, l'énergie, est exprimée en joules si t, le temps, est exprimé en secondes ;
- Ou E, l'énergie, est exprimée en Wattheure si t, le temps, est exprimé en heure.
La loi de Joule
La loi de Joule correspond à une loi qui permet de définir le dégagement d'énergie, dissipée sous forme de chaleur, d'un résistor ou résistance qui se trouve parcouru par un courant électrique. Ainsi, pour une résistance de résistivité R traversée par un courant d'intensité i, on obtient les relations suivantes :  Et donc :
Et donc : 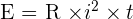 Où :
Où :
- E, représentant l'énergie, est exprimé en joules ;
- R, représentant la résistivité de la résistance, est exprimée en ohms ;
- i, représentant l'intensité du courant, est exprimée en ampères ;
- Et t, représentant le temps, est exprimé en secondes.
L'énergie potentielle électrique

L'énergie potentielle électrique, encore appelée énergie électrostatique, correspond à une énergie potentielle mesurée en joules qui résulte alors des forces de Coulomb. On y associe également la configuration d'un ensemble particulier de charges électriques ponctuelles dans un système défini : on peut parler de champ électrostatique. L'énergie potentielle électrique d'un objet dépendra alors de deux paramètres bien définis qui sont : l'énergie de l'objet et sa position par rapport à d'autres objets qui peuvent être chargés électriquement. Ce type d'énergie, c'est-à-dire l'énergie potentielle électrique, correspond à l'énergie qui est utilisée au sein des condensateurs.
Approfondissement de la notion d'énergie potentielle électrique et ce qui l'entoure
Il est possible de définir un champ électrostatique à partir d'un champ électrique et d'un champ magnétique. Nous vous expliquerons pourquoi dans les paragraphes suivant.
Champ électrique
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance. Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi : 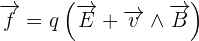 avec :
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude. Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes. Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb. On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet. Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électromagnétique
En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante : 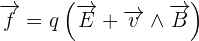 avec :
avec :  le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge  ] le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi. En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude. De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante. D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
] le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi. En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude. De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante. D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Le champ électrostatique
On parle de champ électrostatique lors que les charges qui constitue le champ sont au repos dans le référentiel d'étude. Ce champ est donc déduit de l'expression de la loi de Coulomb, aussi appelée interaction électrostatique.
Loi de Coulomb (1785)
Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés. Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposée et répulsive sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie en raison inverse du carré de la distance r.
Il est alors possible de traduire ces caractéristiques en une formule exprimant la force exercée par q1 sur q2 :  avec :
avec :
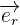 le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2
le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2 la permittivité diélectrique du vide
la permittivité diélectrique du vide
Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance. En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare. Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force et donc d'obtenir la relation suivante : 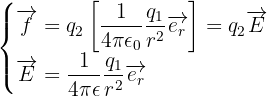 avec :
avec :
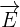 un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance. En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique. Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
C’est vraiment très bien j’aime en tant que technicien en électricité.
Bonjour je voulais savoir comment fessions-nous pour calculer la durée t en sachant P et E ?
Bonjour,
Pour déterminer t en connaissant P et E, il suffit d’isoler cette donnée dans le formule \[ E = P \times t \]. Pour cela, il faut diviser chaque membre de l’équation par P, on obtient alors cette formule : \[ t = \frac E P \]
Pour calculer il suffit juste dapplique la formule
E=p×t