Chapitres
Quand nous disons qu'une bouteille est vide, cela signifie que l'air qui la remplit ne nous semble pas matériel. Pourtant, l'air est de la matière. La matière se caractérise principalement par sa masse. L'air a-t-il une masse ?
Réponse : l'air est pesant mais sa masse est très faible et même si nous ne le ressentons pas, il pèse sur toutes les parties de notre corps.

L'air est un mélange de gaz

L'air est un mélange de gaz. Il contient environ 20 % de dioxygène et 80 % de diazote. Ainsi, 1 l d'air est composé de 0,2 l de dioxygène et de 0,8 l de diazote mélangés. On retrouve la même proportion pour le nombre de particules : dans un volume donné d'air, il y a quatre fois plus de particules de diazote que de particules de dioxygène.
L'air et la propagation du son
Lorsque l'onde se propage dans un milieu fluide compressible, il est possible d'observer une variation de pression qui va alors se propager sous la forme d'une onde. L'air nous entourant étant un milieu fluide compressible, il est alors possible de ressentir ces ondes sous la forme de son que l'on perçoit grâce aux tympans. Cependant, pour qu'elle soit perceptible, il faut que la variation de pression, parce que son amplitude est faible par rapport à la pression atmosphérique, soit suffisamment rapide et répétée.
Il est possible de considérer tout objet vibrant, tel qu'un instrument de musique ou encore un haut-parleur, comme étant une source sonore qui est donc, comme son nom l'indique, la source des vibration de l'air. La perturbation va alors se propager, même si les particules oscillent très peu (soit quelques micromètres autour d'une position stable), d'une façon analogue aux perturbations de l'eau lorsqu'une pierre y tombe : on peut observer des vagues qui s'éloignent peu à peu du point de perturbation bien que l'eau reste au même endroit. En effet, l'eau ne se déplace que verticalement et ne suit pas les vagues (il est possible d'observer ce phénomène en plaçant un objet flottant près de la perturbation : il ne restera à la même position).
On peut alors dire que, dans les fluides, l'onde sonore correspond à une onde longitudinale. Ainsi, les particules observées vibrent de façon parallèle à la direction de déplacement de l'onde.
Une onde sonore peut également être transmise par un solide vibrant. En effet, la vibration va se propager au sein du solide comme dans les fluides : il y aura de faibles oscillation autour de la position d'équilibre des atomes constituant le solide. La conséquence est alors une contrainte du matériau qui, équivalente à la pression dans un fluide, est très difficile à mesurer. C'est donc la rigidité du matériau qui permettra la transmission des ondes de contraintes transversales.
Il peut être intéressant de noter que, la vitesse de propagation du son, également appelée célérité, varie selon différentes propriétés du milieu comme :
- La nature du milieu ;
- La température du milieu ;
- Et la pression du milieu.
Ainsi, dans un gaz parfait, on peut obtenir la vitesse de propagation d'une onde sonore avec la relation suivante :
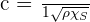
Avec :
- ρ correspondant à la masse volumique du gaz ;
- Et χS correspondant à la compressibilité isentropique du gaz.
Il est également possible d'observer une diminution de la vitesse du son lorsque :
- La densité du gaz augmente, on appelle cela l'effet d'inertie ;
- La compressibilité du gaz, c'est à dire sa capacité à changer de volume selon la pression qu'il subit, augmente.
L'air et la réfraction de la lumière

Définition : La réfraction de la lumière correspond au changement de direction du rayon lumineux lorsque celui-ci traverse une surface séparant deux milieux d'indices de réfraction différents.
En effet, la loi de Snell-Descartes de la réfraction exprime le changement de direction d'un faisceau lumineux lors de la traversée d'une paroi qui sépare deux milieux différents. Il faut d'abord savoir que chaque milieu est caractérisé par sa capacité à « ralentir » la lumière.
On modélise cette caractéristique par son indice de réfraction n qui s'exprime sous la forme :
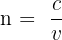
Où v est la vitesse de la lumière dans ce milieu et c est la vitesse de la lumière dans le vide (souvent arrondie à 3.108 m.s-1
Il est important de savoir que :
- Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfractante (appelée dioptre), il est dit réfracté après avoir rencontré cette dernière.
- Le point de rencontre du rayon incident et du dioptre est appelé point d'incidence.
- Le plan contenant le rayon incident et la normale au dioptre, au point d'incidence est dit plan d'incidence.
- L'angle orienté i1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
- L'angle orienté i2 pris entre la normale au point d'incidence et le rayon réfracté est dit angle de réfraction.
- Les angles i1 et i2 sont positifs si ils sont orientés dans le sens trigonométrique (sens inverse des aiguilles d'une montre), négatifs sinon.
On prend n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté.
Pour pouvoir énoncer la loi de la réfraction, il faut que le rayon réfracté, le rayon incident et la normale (au dioptre) soient dans un même plan qui est appelé le plan d'incidence et que le rayon incident et le rayon réfracté soient situés de part et d'autre de la normale.
Lorsque n1 > n2 (et respectivement n1 < n2) le rayon réfracté (et respectivement : incident) se rapproche plus rapidement du dioptre que le rayon incident (ou réfracté). Cependant, il existe un cas particulier où le rayon réfracté (ou incident) se retrouve mathématiquement sur le dioptre (sa limite) : il y a alors réflexion totale.
Comment mieux comprendre les cours de physique chimie ?
L'air est compressible
Lorsqu'on gonfle un ballon de football, son volume reste sensiblement le même alors que la quantité d';air dans le ballon augmente. Étudions plus en détail le phénomène en réalisant l'expérience suivante.
Protocole : bouchons avec le doigt une seringue à moitié remplie d'air, et poussons sur le piston en maintenant la seringue bouchée.
Observation : au début, le piston s'enfonce assez facilement. À partir du moment où le volume de l'air à l'intérieur de la seringue est divisé par deux, la poussée devient difficile. De même, si nous tirons le piston, nous arrivons difficilement à doubler le volume d'air
Interprétation : dans les deux cas, la seringue étant bouchée, la quantité d'air ne varie pas. Par contre, le volume de l'air emprisonné peut augmenter ou diminuer.
L'air et les gaz sont compressibles ; ils n'ont pas de volume propre. Une même quantité d'air peut occuper des volumes différents. Dans un gaz, les particules sont éloignées les unes des autres et il est possible de les rapprocher ou de les éloigner davantage en modifiant l'espace qu'elles occupent.
Intéressé par un cours physique chimie 3ème ?
La pression de l'air

Dans l'expérience précédente, nous avons pu voir que l'air est compressible, mais qu'il y a une limite à la compression. Cette limite est atteinte lorsque la pression que nous exerçons sur le piston est aussi forte que la pression de l'air à l'intérieur de la seringue. La pression est due aux particules d'air situées dans la seringue. Agitées, elles rebondissent sur les parois de la seringue et poussent le piston. En diminuant le volume d'air, on augmente la pression dans la seringue : les particules toujours aussi nombreuses et en mouvement se retrouvent avec moins de place. Il est donc plus difficile d'appuyer sur le piston.
Lors de la compression de l'air dans la seringue, la pression à l'intérieur est supérieure à la pression atmosphérique. Si on lâche le piston, seules ces deux pressions s'appliquent sur le celui-ci et c'est la plus forte qui provoque le mouvement du piston revenant alors à sa position initiale.
Remarque : la pression atmosphérique est due aux particules d'air de l'atmosphère. Elle s'exerce sur tous les corps à l'air libre. Sa valeur est de 1 atmosphère ou 1 015 hPa (hectopascal) au niveau de la mer.
La pression correspond à une grandeur physique qui permet de traduire les échange de quantité de mouvement au sein d'un système thermodynamique, notamment au sein d'un solide ou encore d'un fluide. On peut alors définir la pression comme correspondant à l'intensité de force que va exercer une fluide par unité de surface.
La pression est une grandeur scalaire, voire tensorielle, intensive.
Il faut être prudent lorsque l'on parle de la pression. En effet, nombreux sont ceux qui parlent de pression exercée par un fluide sur une paroi pour parler de la force pressante que le fluide va exercer par unité d'aire de la paroi. Cependant, la force correspond plutôt à une grandeur vectorielle que l'on défini localement alors que la pression correspond à une grandeur scalaire qui est définie en tout point du fluide concerné.
Les unités de pression
L'unité de pression est le Pascal noté (Pa), même si l'on parle parfois du Bar qui, lui, n'est pas une unité du Système International.
L'analyse dimensionnelle de la pression permet de montrer que celle-ci est homogène à une force surfacique (1 Pa = 1 N/m²) comme à une énergie volumique (1 Pa = 1 J/m3).
Quelques formules
La pression p, le volume V, la quantité de matière n, et la température T d'un gaz sont liés par :
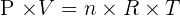
Avec R = 8,31 USI
Le volume molaire d'un gaz Vm est le volume occupé par 1 mole de ce gaz dans des conditions de température et de pression donnés. On peut déterminer ainsi le volume molaire par la formule suivante : 
En sachant que Vm s'exprime en L.mol-1
Pour ce qui est des gaz, le volume V et la quantité de matière n sont liés par : 
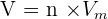
La quantité de mouvement
En physique, on appelle la quantité de mouvement tout produit de la masse par le vecteur vitesse d'un corps matériel que l'on suppose ponctuel. Ainsi, la quantité de mouvement correspond à une grandeur vectorielle que l'on définit par 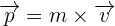 qui dépendra du référentiel d'étude.
qui dépendra du référentiel d'étude.
De plus, en utilisant l'additivité, on est capable de définir la quantité de mouvement d'un corps non ponctuel ou système matériel. De ce fait, il devient possible de démontrer que la quantité de matière est égale à la quantité de mouvement du centre d'inertie de l'objet étudié affecté de la masse totale du système. On a donc 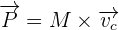 où C correspond au centre d'inertie. On utilise le kg.m.s-1 comme unité.
où C correspond au centre d'inertie. On utilise le kg.m.s-1 comme unité.
De façon logique et naturelle, la notion de quantité de mouvement s'introduit en dynamique. En effet, la relation fondamentale de la dynamique exprime le fait que l'action d'une force extérieure sur un système conduit à une variation de sa quantité de mouvement par l'expression suivante : 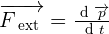
On peut également dire de la notion de quantité de mouvement qu'elle fait partie, de la même façon que l'énergie, des grandeurs qui se conservent dans un système isolé et donc un système qui n'est soumis à aucune action extérieure ou alors ces mêmes actions extérieures sont négligeables ou se compensent. On utilise d'ailleurs fréquemment cette propriété en théorie des collisions.
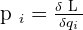 .
.
Dans le cas d'un champ électromagnétique, on appelle la quantité de mouvement impulsion. Elle fait alors référence à la densité volumique d'impulsion du champ donné par la formule : 
La masse de l'air

Effectuons l'expérience suivante pour montrer que l'air a bien une masse.
Protocole : mesurons avec une balance de précision la masse m1 d'un ballon de football suffisamment gonflé pour qu'il garde le même volume une fois plus gonflé. Gonflons ensuite le ballon et mesurons sa masse m2.
Résultats : on trouve m1 = 326,2 g et m2 = 327,1 g.
Interprétation : la différence des deux masses est égale à la masse de l'air ajouté dans le ballon. L'air est pesant, il a une masse. En réalisant des expériences plus précises, nous trouverions que la masse de 1 l d'air est de 1,293 g.
En physique, la masse correspond à une grandeur physique positive et intrinsèque d'un corps.
De façon plus précise, en physique newtonienne, la masse correspond à une grandeur extensive. Cela signifie alors que la masse d'un corps formé de parties correspond à la somme des masses de ces différentes parties qui le compose.
De plus, il est essentiel de noter que la masse est une grandeur conservative. De ce fait, elle reste constante dans le cas d'un système isolé qui n'échange donc pas de matière avec son environnement.
Pour une espèce donnée, la masse m, la quantité de matière n et la masse molaire M sont liés par : 
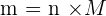
Les propriétés
La masse peut se manifester au travers de deux propriétés fondamentales :
En effet, en mécanique statique, la masse est correspond à l'un des premières grandeurs facilement mesurable par les gens via le système de pesée puisque celle-ci permet de comparer la masse de l'objet défini avec un masse étalon connue. On appellera alors ce système la masse pesante. C'est ainsi que l'on liera la quantité de matière d'un corps à sa masse.
Tandis qu'en mécanique dynamique, la masse correspond à une grandeur qui intervient dans le principe fondamental de la dynamique comme étant la résistance de la matière au changement de vitesse. En effet, plus la masse d'un corps est importante, plus il faudra exercer une force important pour modifier la direction ou encore sa vitesse. On appelle alors ce phénomène "masse inerte".
Ainsi, cet aspect de la masse présente un rôle essentiel dans tous les domaines de la dynamique puisqu'elle correspond à une notion présente dans grand nombre de relations de physique classique ou encore dans les calculs qui permettent de les définir. En effet, il est possible de constater une proportionnalité entre la masse inerte et la masse pesante et cela de façon totalement indépendante de la nature du matériau mis en jeu. Cela permet alors de prendre la même unité pour la masse pesante et la masse inerte et donc de pouvoir les définir comme étant égale. Ainsi, cette équivalence à permis de définir un principe d'équivalence.
L'unité
L'unité de masse est le kilogramme dans le Système international d'unités (S.I.).
Comme pour le litre il existe des sous-unités : kg ; hg ; dag ; g ; dg ; cg ; mg .
Attention à ne pas faire comme une majorité et confondre la masse avec le poids. En effet, dans le vocabulaire de la physique, le poids correspond à la force exercée par la gravité sur un corps pesant.
La masse se mesure avec une balance
Balance de Roberval
C'est généralement avec cet outil qu'on vous a sensibilisé en école primaire à la notion de masse bien que, très souvent, les professeurs sèment la confusion en utilisant le terme de "poids" alors méfiez-vous de ce que vous pensez savoir !
La balance de Roberval à deux fléaux correspond à un instrument de pesage nommé ainsi en hommage à son inventeur qui n'est d'autre que Gilles Personne de Roberval, un célèbre mathématicien mais aussi physicien français né en 1602.
Petite anecdote amusante, ce scientifique est connu sous le nom de Roberval puisque celui-ci était originaire de Roberval dans l'Oise.
Le mathématicien Gille Personne a inventé cette balance lorsqu'il a eu l'idée de place des plateaux au dessus du fléau alors que, de façon traditionnelle, ces plateaux étaient suspendus en dessous du fléau. Ainsi, Le principe de l'énigme statique expliquant que les position des masses sur les plateaux ne perturbent pas le résultat final de la mesure, sera présenté sous la forme de thèse devant l'Académie royale des sciences par Gilles Personne de Roberval en 1669.
Balance électronique
Cette balance correspond à ce que vous trouverez certainement dans vos cuisines. Un plateau unique avec un écran indiquant la mesure avec une précision dépendant de l'appareil.
A noter que la balance la plus sensible au monde a vu le jour en 2012 par des chercheurs de l’Institut Catalan de Nanotechnologie. Celle-ci permet de peser au yoctogramme près.
La masse de l'objet dépend de la densité de l'objet mais également du volume
A noter que déclarer que 1 Litre pèse 1 Kilogramme est totalement faux. En effet, un litre d'huile pèse 800 g et non pas 1 kg.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !